题目内容
8．角A，B，C所对应的边分别为a，b，c．已知bcosC+ccosB=4b，则$\frac{a}{b}$=4．分析 已知等式利用正弦定理化简，再利用两角和与差的正弦函数公式及诱导公式化简，再利用正弦定理变形即可得到结果．
解答 解：将bcosC+ccosB=4b，利用正弦定理化简得：sinBcosC+sinCcosB=4sinB，
即sin（B+C）=4sinB，
∵sin（B+C）=sinA，
∴sinA=4sinB，
利用正弦定理化简得：a=4b，
则$\frac{a}{b}$=4．
故答案为：4．
点评 此题考查了正弦定理，以及两角和与差的正弦函数公式，熟练掌握正弦定理是解本题的关键，属于中档题．
练习册系列答案
相关题目
19．如图，网格纸上的小正方形边长都为4，粗线画出的是某几何体的三视图，则该几何体的体积为（ ）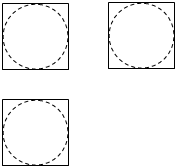
| A． | 64-$\frac{32}{3}$π | B． | 64-$\frac{96\sqrt{3}}{3}$π | C． | 64-$\frac{64\sqrt{2}}{3}$π | D． | 64-16π |
16．某中学进行了该学年度期末统一考试，该校为了了解高一年级1 000名学生的考试成绩，从中随机抽取了100名学生的成绩单，就这个问题来说，下面说法正确的是（ ）
| A． | 1 000名学生是总体 | B． | 每个学生是个体 | ||
| C． | 1 000名学生的成绩是一个个体 | D． | 样本的容量是100 |
13．
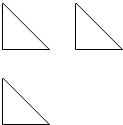某几何体的三视图如图所示（均为直角边长为2的等腰直角三角形），则该几何体的表面积为（ ）
某几何体的三视图如图所示（均为直角边长为2的等腰直角三角形），则该几何体的表面积为（ ）| A． | 4+4$\sqrt{2}$ | B． | 4+4$\sqrt{3}$ | C． | 6+2$\sqrt{3}$ | D． | 8 |