题目内容
8.已知函数f(x)=a-x2(1≤x≤2)与g(x)=x+2的图象上存在关于x轴对称的点,则实数a的取值范围是( )| A. | [-2,0] | B. | [-$\frac{9}{4}$,0] | C. | [2,4] | D. | [-$\frac{9}{4}$,+∞) |
分析 由已知,得到方程a-x2=-(x+2)?a=x2-x-2在区间[1,2]上有解,构造函数h(x)=x2-x-2,求出它的值域,得到a的范围即可
解答 解:若函数f(x)=a-x2(1≤x≤2)与g(x)=x+2的图象上存在关于x轴对称的点,
则方程a-x2=-(x+2)?a=x2-x-2在区间[1,2]上有解,
令h(x)=x2-x-2,1≤x≤2,
由h(x)=x2-x-2的图象是开口朝上,且以直线x=$\frac{1}{2}$为对称轴的抛物线,
故当x=1时,h(x)取最小值-2,当x=2时,函数取最大值0,
故a∈[-2,0],
故选:A.
点评 本题考查了构造函数法求方程的解及参数范围;考查了转化、数形结合思想,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.已知A(-2,0),B(2,0),斜率为k的直线l上存在不同的两点M,N满足:|MA|-|MB|=2$\sqrt{3}$,|NA|-|NB|=2$\sqrt{3}$,且线段MN的中点为(6,1),则k的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
19.春天来了,某学校组织学生外出踏青.4位男生和3位女生站成一排合影留念,男生甲和乙要求站在一起,3位女生不全站在一起,则不同的站法种数是( )
| A. | 964 | B. | 1080 | C. | 1152 | D. | 1296 |
3.已知点P(x,y)的坐标满足约束条件$\left\{\begin{array}{l}{x+y≤3}\\{y≤3x}\\{x+2y-2≥0}\end{array}\right.$,O为坐标原点,则|$\overrightarrow{OP}$|的最小值等于( )
| A. | 1 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\sqrt{5}$ |
13.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若点F2关于直线bx-ay=0的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
20.5位大学毕业生分配到3家单位,每家单位至少录用1人,则不同的分配方法共有( )
| A. | 25种 | B. | 60种 | C. | 90种 | D. | 150种 |
18.函数y=$\frac{2-x}{x+1}$,x∈(m,n]最小值为0,则m的取值范围是( )
| A. | (1,2) | B. | (-1,2) | C. | [1,2) | D. | [-1,2) |
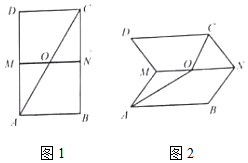 如图1,2,已知ABCD是矩形,M,N分别为边AD,BC的中点,MN与AC交于点O,沿MN将矩形MNCD折起,设AB=2,BC=4,二面角B-MN-C的大小为θ.
如图1,2,已知ABCD是矩形,M,N分别为边AD,BC的中点,MN与AC交于点O,沿MN将矩形MNCD折起,设AB=2,BC=4,二面角B-MN-C的大小为θ.