题目内容
3．已知点P（x，y）的坐标满足约束条件$\left\{\begin{array}{l}{x+y≤3}\\{y≤3x}\\{x+2y-2≥0}\end{array}\right.$，O为坐标原点，则|$\overrightarrow{OP}$|的最小值等于（ ）| A． | 1 | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{2\sqrt{5}}{5}$ | D． | $\sqrt{5}$ |
分析 由约束条件作出可行域，再由$|\overrightarrow{OP}|=\sqrt{{x}^{2}+{y}^{2}}$的几何意义，即原点到直线的距离求解．
解答 解：∵P（x，y），∴$|\overrightarrow{OP}|=\sqrt{{x}^{2}+{y}^{2}}$，
由约束条件$\left\{\begin{array}{l}{x+y≤3}\\{y≤3x}\\{x+2y-2≥0}\end{array}\right.$作出可行域如图，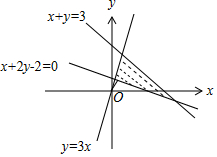
原点O到直线x+2y-2=0的距离d=$\frac{|-2|}{\sqrt{{1}^{2}+{2}^{2}}}=\frac{2\sqrt{5}}{5}$．
∴|$\overrightarrow{OP}$|的最小值等于$\frac{2\sqrt{5}}{5}$．
故选：C．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
13．若将函数y=3cos（2x+$\frac{π}{2}$）的图象向右平移$\frac{π}{6}$个单位长度，则平移后图象的一个对称中心是（ ）
| A． | （$\frac{π}{6}$，0） | B． | （-$\frac{π}{6}$，0） | C． | （$\frac{π}{12}$，0） | D． | （-$\frac{π}{12}$，0） |
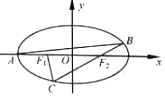如图，设点A，F1，F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左，右焦点，过点A作斜率为k的直线交椭圆于另一点B，连接BF2并延长交椭圆于点C．
8．已知函数f（x）=a-x2（1≤x≤2）与g（x）=x+2的图象上存在关于x轴对称的点，则实数a的取值范围是（ ）
| A． | [-2，0] | B． | [-$\frac{9}{4}$，0] | C． | [2，4] | D． | [-$\frac{9}{4}$，+∞） |