题目内容
17.(x+2y)(x-y)7展开式中,含x3y5项的系数是49.分析 由(x+2y)(x-y)7=(x+2y)$[{x}^{7}-7{x}^{6}y+…+{∁}_{7}^{4}{x}^{3}(-y)^{4}+$${∁}_{7}^{5}{x}^{2}(-y)^{5}$+…].即可得出含x3y5项的系数是2${∁}_{7}^{4}$-${∁}_{7}^{5}$.
解答 解:(x+2y)(x-y)7=(x+2y)$[{x}^{7}-7{x}^{6}y+…+{∁}_{7}^{4}{x}^{3}(-y)^{4}+$${∁}_{7}^{5}{x}^{2}(-y)^{5}$+…].
含x3y5项的系数是2${∁}_{7}^{4}$-${∁}_{7}^{5}$=49.
故答案为:49.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
7.集合$M=\left\{{\left.x\right|x=\frac{n}{2}+1,n∈Z}\right\}$,$N=\left\{{\left.y\right|y=m+\frac{1}{2},m∈Z}\right\}$,则两集合M,N的关系为( )
| A. | M∩N=∅ | B. | M=N | C. | M?N | D. | N?M |
8.已知函数f(x)=a-x2(1≤x≤2)与g(x)=x+2的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | [-2,0] | B. | [-$\frac{9}{4}$,0] | C. | [2,4] | D. | [-$\frac{9}{4}$,+∞) |
5.关于函数f(x)=2cos2$\frac{x}{2}$+$\sqrt{3}$sinx(x∈[0,π])下列结论正确的是( )
| A. | 有最大值3,最小值-1 | B. | 有最大值2,最小值-2 | ||
| C. | 有最大值3,最小值0 | D. | 有最大值2,最小值0 |
2.在△ABC中,角A,B,C的对边分别是a,b,c,若$\frac{a}{sinB}+\frac{b}{sinA}=2c$,则A=( )
| A. | 45° | B. | 30° | C. | 60° | D. | 90° |
9.已知集合$M=\left\{{x\left|{\frac{x-2}{x-3}<0}\right.}\right\},N=\left\{{x\left|{{{log}_{\frac{1}{2}}}(x-2)≥1}\right.}\right\}$,则M∩N=( )
| A. | $[{\frac{5}{2},3})$ | B. | $({2,\frac{5}{2}}]$ | C. | $[{2,\frac{5}{2}}]$ | D. | $({\frac{5}{2},3})$ |
7.设等差数列{an}的前n项和为Sn,已知${({{a_5}-1})^3}+3{a_5}=4$,${({{a_8}-1})^3}+3{a_8}=2$,则下列选项正确的是( )
| A. | S12=12,a5>a8 | B. | S12=24,a5>a8 | C. | S12=12,a5<a8 | D. | S12=24,a5<a8 |
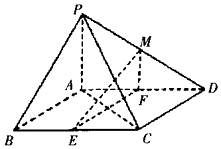 在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=135°,PA⊥底面ABCD,AB=AC=PA=1,E,F分別是BC,AD的中点,点M在线段PD上.
在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=135°,PA⊥底面ABCD,AB=AC=PA=1,E,F分別是BC,AD的中点,点M在线段PD上.