题目内容
18.函数y=$\frac{2-x}{x+1}$,x∈(m,n]最小值为0,则m的取值范围是( )| A. | (1,2) | B. | (-1,2) | C. | [1,2) | D. | [-1,2) |
分析 化简函数为y=$\frac{3}{x+1}$-1,根据函数y的单调性以及y在x∈(m,n]时取得最小值0,求出m的取值范围.
解答 解:函数y=$\frac{2-x}{x+1}$=$\frac{3-x-1}{x+1}$=$\frac{3}{x+1}$-1,
且在x∈(-1,+∞)时,函数y是单调递减函数,
在x=2时,y取得最小值0;
根据题意x∈(m,n]时y的最小值为0,
∴m的取值范围是-1≤m<2.
故选:D.
点评 本题考查了反比例型的函数单调性与最值的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知函数f(x)=a-x2(1≤x≤2)与g(x)=x+2的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | [-2,0] | B. | [-$\frac{9}{4}$,0] | C. | [2,4] | D. | [-$\frac{9}{4}$,+∞) |
9.已知集合$M=\left\{{x\left|{\frac{x-2}{x-3}<0}\right.}\right\},N=\left\{{x\left|{{{log}_{\frac{1}{2}}}(x-2)≥1}\right.}\right\}$,则M∩N=( )
| A. | $[{\frac{5}{2},3})$ | B. | $({2,\frac{5}{2}}]$ | C. | $[{2,\frac{5}{2}}]$ | D. | $({\frac{5}{2},3})$ |
13.若直线ax+by+1=0(a>0,b>0)把圆(x+4)2+(y+1)2=16分成面积相等的两部分,则$\frac{1}{2a}+\frac{2}{b}$的最小值为( )
| A. | 10 | B. | 8 | C. | 5 | D. | 4 |
10.已知a∈R,若$f(x)=(\frac{1}{x}+a){e^x}$在区间(0,1)上有且只有一个极值点,则a的取值范围是( )
| A. | a<0 | B. | a>0 | C. | a≤1 | D. | a≥0 |
7.设等差数列{an}的前n项和为Sn,已知${({{a_5}-1})^3}+3{a_5}=4$,${({{a_8}-1})^3}+3{a_8}=2$,则下列选项正确的是( )
| A. | S12=12,a5>a8 | B. | S12=24,a5>a8 | C. | S12=12,a5<a8 | D. | S12=24,a5<a8 |
8.已知各项均为正数的等比数列{an}的前n项之积为Tn,且a2=8,a1•a7=4,则当Tn最大时,n的值为( )
| A. | 5或6 | B. | 6 | C. | 5 | D. | 4或5 |
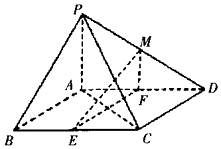 在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=135°,PA⊥底面ABCD,AB=AC=PA=1,E,F分別是BC,AD的中点,点M在线段PD上.
在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=135°,PA⊥底面ABCD,AB=AC=PA=1,E,F分別是BC,AD的中点,点M在线段PD上.