题目内容
20.5位大学毕业生分配到3家单位,每家单位至少录用1人,则不同的分配方法共有( )| A. | 25种 | B. | 60种 | C. | 90种 | D. | 150种 |
分析 根据题意,分2步进行分析:①、先把5位大学毕业生分成3组,②、将分好的3组全排列,对应3家单位,分别求出每一步的情况数目,由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析:
①、先把5位大学毕业生分成3组,
若分成2-2-1的三组,有$\frac{{C}_{5}^{2}{C}_{3}^{2}{C}_{1}^{1}}{{A}_{2}^{2}}$=15种,
若分成3-1-1的三组,有$\frac{{C}_{5}^{3}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}}$=10种,
则一共有15+10=25种分组方法;
②、将分好的3组全排列,对应3家单位,有A33=6种情况,
则不同的分配方法有25×6=150种;
故选:D.
点评 本题考查排列、组合的综合应用,注意先分好组,再对应3家单位.

练习册系列答案
相关题目
8.已知函数f(x)=a-x2(1≤x≤2)与g(x)=x+2的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | [-2,0] | B. | [-$\frac{9}{4}$,0] | C. | [2,4] | D. | [-$\frac{9}{4}$,+∞) |
5.关于函数f(x)=2cos2$\frac{x}{2}$+$\sqrt{3}$sinx(x∈[0,π])下列结论正确的是( )
| A. | 有最大值3,最小值-1 | B. | 有最大值2,最小值-2 | ||
| C. | 有最大值3,最小值0 | D. | 有最大值2,最小值0 |
9.已知集合$M=\left\{{x\left|{\frac{x-2}{x-3}<0}\right.}\right\},N=\left\{{x\left|{{{log}_{\frac{1}{2}}}(x-2)≥1}\right.}\right\}$,则M∩N=( )
| A. | $[{\frac{5}{2},3})$ | B. | $({2,\frac{5}{2}}]$ | C. | $[{2,\frac{5}{2}}]$ | D. | $({\frac{5}{2},3})$ |
10.已知a∈R,若$f(x)=(\frac{1}{x}+a){e^x}$在区间(0,1)上有且只有一个极值点,则a的取值范围是( )
| A. | a<0 | B. | a>0 | C. | a≤1 | D. | a≥0 |
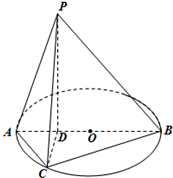 如图,已知PD垂直于以AB为直径的圆O所在的平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.
如图,已知PD垂直于以AB为直径的圆O所在的平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.