题目内容
已知函数f（x）=| 3 |
| ωx |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
（Ⅰ）求ω与a的值；
（Ⅱ）若f（x0）=
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
考点：三角函数中的恒等变换应用,由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的求值,三角函数的图像与性质
分析：（Ⅰ）首先通过三角函数的恒等变换求出函数的正弦型函数的形式，进一步利用函数的图象求出函数的周期和最值，进一步确定函数的解析式．
（Ⅱ）利用上步结论，对函数的角进行恒等变换，进一步利用函数的定义域求出函数的值，最后利用函数的值求出最终结果．
（Ⅱ）利用上步结论，对函数的角进行恒等变换，进一步利用函数的定义域求出函数的值，最后利用函数的值求出最终结果．
解答：
解：（Ⅰ）f（x）=
cos2
+
asinωx-
a
=asin（ωx+
）
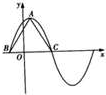
由函数的图象得：BC=4=
则：T=8
所以：ω=
=
所以：a=BAsin
=2
；
（Ⅱ）由（Ⅰ）得：f（x）=2
sin(
x+
)
所以：f(x0)=2
sin(
x0+
)=
解得：sin(
x0+
)=
x0∈(-
，
)
所以：
x0+
∈(-
，
)
所以：cos(
x0+
)=
f（x0-1）=2
sin[(
x0+
-
)
=2
（
•
-
•
）
=
．
| 3 |
| ωx |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=asin（ωx+
| π |
| 3 |
由函数的图象得：BC=4=
| T |
| 2 |
则：T=8
所以：ω=
| 2π |
| 8 |
| π |
| 4 |
所以：a=BAsin
| π |
| 3 |
| 3 |
（Ⅱ）由（Ⅰ）得：f（x）=2
| 3 |
| π |
| 4 |
| π |
| 3 |
所以：f(x0)=2
| 3 |
| π |
| 4 |
| π |
| 3 |
8
| ||
| 5 |
解得：sin(
| π |
| 4 |
| π |
| 3 |
| 4 |
| 5 |
x0∈(-
| 10 |
| 3 |
| 2 |
| 3 |
所以：
| π |
| 4 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
所以：cos(
| π |
| 4 |
| π |
| 3 |
| 3 |
| 5 |
f（x0-1）=2
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
=2
| 3 |
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| ||
| 2 |
=
| ||
| 5 |
点评：本题考查的知识要点：三角函数关系式的恒等变换，利用函数的图象求函数的关系式，利用函数的定义域求函数的值域，进一步求函数的值．属于基础题型．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
如图，圆O是△ABC的外接圆，∠BAC的平分线交BC于点F，D是AF的延长线与⊙O的交点，AC的延线与⊙O的切线DE交于点E．