题目内容
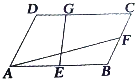
如图，在?ABCD中，
=
，
=
，E、F分别是AB、BC的中点，G点使
=
，试以
，
为基底表示向量
与
．
| AB |
| a |
| AD |
| b |
| DG |
| 1 |
| 3 |
| DC |
| a |
| b |
| AF |
| EG |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由平行四边形性质可得：
=
，
=
．再利用向量的多边形法则、向量共线定理即可得出．
| DC |
| AB |
| BC |
| AD |
解答：
解：由平行四边形性质可得：
=
，
=
．
∴
=
+
=
+
=
+
．
=
+
+
=-
+
+
=
-
=
-
．
| DC |
| AB |
| BC |
| AD |
∴
| AF |
| AB |
| BF |
| AB |
| 1 |
| 2 |
| BC |
| a |
| 1 |
| 2 |
| b |
| EG |
| EA |
| AD |
| DG |
| 1 |
| 2 |
| AB |
| AD |
| 1 |
| 3 |
| DC |
| AD |
| 1 |
| 6 |
| AB |
| b |
| 1 |
| 6 |
| a |
点评：本题考查了平行四边形性质、向量的多边形法则、向量共线定理，属于基础题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
设
、
是平面内所有向量的一组基底，则下面四组向量中，不能作为基底的是（ ）
| e1 |
| e2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、2
|
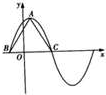已知函数f（x）=
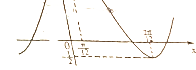方程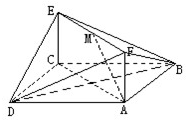
如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=