题目内容
已知x,y∈R且
,则存在θ∈R,使得(x-4)cosθ+ysinθ+
=0的概率为 .
|
| 2 |
考点:简单线性规划
专题:概率与统计
分析:作出不等式组对应的平面区域,利用辅助角公式将条件进行化简,求出对应的平面区域的面积即可得到结论.
解答:
解:∵(x-4)cosθ+ysinθ+
=0,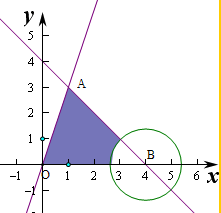
∴(4-x)cosθ-ysinθ=
,
即
cos(θ+β)=
,(β为参数),
∵存在θ∈R,使得(x-4)cosθ+ysinθ+
=0,
∴
≥
,
即(x-4)2+y2≥2,对应的图象是以(4,0)为圆心,半径r=
的圆的外部,
作出不等式组对应的平面区域如图,
则由
,解得
,即A(1,3),
则△AOB的面积S=
×4×3=6,
圆在△AOB内部的面积S=
×(
)2×
=
,
则(x-4)2+y2≥2,对应的区域面积S=6-
,
则对应的概率P=
=1-
,
故答案为:1-
| 2 |

∴(4-x)cosθ-ysinθ=
| 2 |
即
| (4-x)2+y2 |
| 2 |
∵存在θ∈R,使得(x-4)cosθ+ysinθ+
| 2 |
∴
| (4-x)2+y2 |
| 2 |
即(x-4)2+y2≥2,对应的图象是以(4,0)为圆心,半径r=
| 2 |
作出不等式组对应的平面区域如图,
则由
|
|
则△AOB的面积S=
| 1 |
| 2 |
圆在△AOB内部的面积S=
| 1 |
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
则(x-4)2+y2≥2,对应的区域面积S=6-
| π |
| 4 |
则对应的概率P=
6-
| ||
| 6 |
| π |
| 24 |
故答案为:1-
| π |
| 24 |
点评:本题主要考查几何概型的概率计算,根据三角函数的辅助角公式结合线性规划的知识是解决本题的关键.

练习册系列答案
相关题目
已知等比数列{an}的公比为2,前4项的和是2,则前8项的和为( )
| A、16 | B、31 | C、34 | D、32 |