题目内容
已知a2sin θ+acos θ-2=0,b2sin θ+bcos θ-2=0(a,b,θ∈R,且a≠b),直线l过点A(a,a2),B(b,b2),则直线l被圆(x-cos θ)2+(y-sin θ)2=4所截得的弦长为________.
2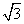
解题思路:据已知a,b可视为方程x2sin θ+xcos θ-2=0的两根,由韦达定理可得a+b=- ,ab=-
,ab=- ,又因为直线AB的方程为y=(a+b)x-ab,故圆心到直线距离d=
,又因为直线AB的方程为y=(a+b)x-ab,故圆心到直线距离d= =1,故所求弦长为2
=1,故所求弦长为2 =2
=2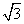 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
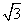 ,BC=2
,BC=2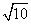
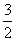 (an-1),数列{bn}满足bn=
(an-1),数列{bn}满足bn=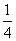 bn-1-
bn-1- (n≥2),且b1=3.
(n≥2),且b1=3. 时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数y=f
时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数y=f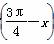 是( )
是( )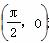 对称
对称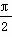 对称
对称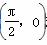 对称
对称 ≤k恒成立,求k的取值范围.
≤k恒成立,求k的取值范围.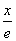 +
+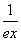 (e≈2.718…).
(e≈2.718…). >0;
>0; =________.
=________.