题目内容
设集合A={x|
≤2x≤32},B={x|2mx-1>0,m≥0}.
(1)当x∈Z时,求A的非空真子集的个数;
(2)若A∩B=∅,求实数m的取值范围.
| 1 |
| 4 |
(1)当x∈Z时,求A的非空真子集的个数;
(2)若A∩B=∅,求实数m的取值范围.
考点:集合的包含关系判断及应用,元素与集合关系的判断
专题:集合
分析:(1)解指数不等式可求出集合A,结合x∈Z可求出A中集合个数,进而得到A的非空真子集的个数;
(2)m=0时,B=∅满足A∩B=∅,m>0 时,所以B=(
,+∞),若A∩B=∅,则
≥5,综合可得实数m的取值范围.
(2)m=0时,B=∅满足A∩B=∅,m>0 时,所以B=(
| 1 |
| 2m |
| 1 |
| 2m |
解答:
解:(1)∵集合A={x|
≤2x≤32}=[-2,5],
当x∈Z时,A={-2,-1,0,1,2,3,4,5},
即A中含有8个元素,
∴A的非空真子集数为28-2=254个.
(2)①m=0时,B=∅满足A∩B=∅,
②当m>0 时,B=(
,+∞),
若A∩B=∅,则
≥5,
∴0<m≤
,
综上所述,知m的取值范围是:[0,
]
| 1 |
| 4 |
当x∈Z时,A={-2,-1,0,1,2,3,4,5},
即A中含有8个元素,
∴A的非空真子集数为28-2=254个.
(2)①m=0时,B=∅满足A∩B=∅,
②当m>0 时,B=(
| 1 |
| 2m |
若A∩B=∅,则
| 1 |
| 2m |
∴0<m≤
| 1 |
| 10 |
综上所述,知m的取值范围是:[0,
| 1 |
| 10 |
点评:本题考查的知识点是集合的包含关系判断及应用,元素与集合关系的判断,(1)的关键是判断A中元素个数,(2)中易忽略m=0的情况.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.
如图,正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.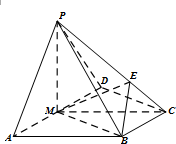 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD是直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,CD=
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD是直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,CD=
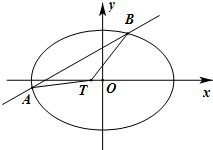 如图,椭圆C:
如图,椭圆C: