题目内容
在△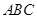 中,内角
中,内角 所对的边分别为
所对的边分别为 ,已知m
,已知m ,n
,n ,m·n
,m·n .
.
(1)求 的大小;
的大小;
(2)若 ,
, ,求△
,求△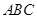 的面积.
的面积.
(1)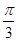 ;(2)
;(2)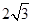 .
.
解析试题分析:(1)由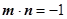 ,结合向量数量积的定义,可得关于
,结合向量数量积的定义,可得关于 的三角函数关系式,然后对三角函数关系式进行适当变形处理,直到能求出
的三角函数关系式,然后对三角函数关系式进行适当变形处理,直到能求出 的某个三角函数即可;(2)本题本质上就是一个解三角形的问题,沟通三角形中的边角关系主要是正弦定理和余弦定理,在
的某个三角函数即可;(2)本题本质上就是一个解三角形的问题,沟通三角形中的边角关系主要是正弦定理和余弦定理,在 中,已知
中,已知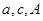 ,求其面积,可先用余弦定理求出
,求其面积,可先用余弦定理求出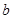 ,再用面积公式求出面积,也可先用正弦定理求出
,再用面积公式求出面积,也可先用正弦定理求出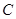 ,再得
,再得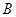 ,进而用三角形面积公式求出面积.
,进而用三角形面积公式求出面积.
试题解析:解:(1)法一:由题意知m·n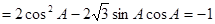 .
.
∴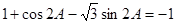 . 即
. 即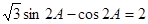 ,∴
,∴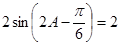 ,即
,即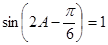 .
.
∵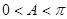 ,∴
,∴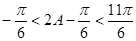 ,∴
,∴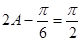 ,即
,即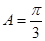 .
.
法二:由题意知m·n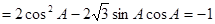 .
.
∴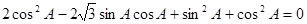 即
即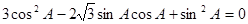 .
.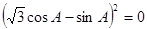 ∴
∴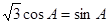 ,即
,即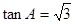 ,∵
,∵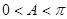 ,∴
,∴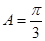 .
.
(2)法一:由余弦定理知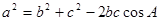 ,即
,即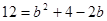 ,
,
∴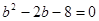 ,解得
,解得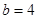 ,(
,(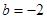 舍去)
舍去)
∴△ 的面积为
的面积为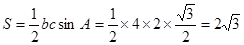 .
.
法二:由正弦定理可知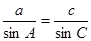 ,所以
,所以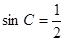 ,因为
,因为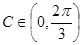
所以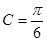 ,
,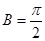 .∴△
.∴△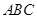 的面积为
的面积为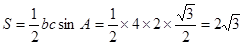

练习册系列答案
相关题目
 中,已知
中,已知 ,求边
,求边 的长及
的长及 中,角A、B,C,所对的边分别为
中,角A、B,C,所对的边分别为 ,且
,且
 的值;
的值; ,求
,求 中,角
中,角 的对边分别为
的对边分别为 .已知
.已知 .
. ;
; ,
, ,且
,且 ,求
,求 .
. ,设函数
,设函数 +1
+1 ,
,  ,求
,求 的值;
的值; ,且满足
,且满足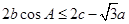 ,求
,求
 中,角
中,角 所对的边分别为
所对的边分别为 ,设
,设 ,
, ,记
,记 .
. 的取值范围;
的取值范围; 与
与 的夹角为
的夹角为 ,
, ,
, ,求
,求 的值.
的值. 的最大值为2.
的最大值为2. 在
在 上的单调递减区间;
上的单调递减区间; 中,
中, ,角
,角 所对的边分别是
所对的边分别是 ,且
,且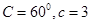 ,求
,求 ,BC=1,P为△ABC内一点,∠BPC=90°
,BC=1,P为△ABC内一点,∠BPC=90°
 ,求PA;
,求PA; ,
, ,
, ,
, ,
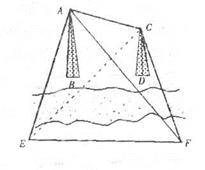
, 请你用文字和公式写出计算A、C之间距离的步骤和结果.
请你用文字和公式写出计算A、C之间距离的步骤和结果.