题目内容
15.已知下列命题(其中a,b为直线,α为平面):①若一条直线垂直于平面内无数条直线,则这条直线与这个平面垂直;
②若一条直线平行于一个平面,则垂直于这条直线的直线一定垂直于这个平面;
③若a∥α,b⊥α,则a⊥b;
④若a⊥b,则过b有惟一α与a垂直.
上述四个命题中,是真命题的有③④.(填序号)
分析 ①平面内无数条直线均为平行线时,不能得出直线与这个平面垂直,故①错误;②垂直于这条直线的直线与这个平面可以是任何的位置关系,故②错误.若a∥α,b⊥α,则根据线面平行、垂直的性质,必有a⊥b.
解答 解:①平面内无数条直线均为平行线时,不能得出直线与这个平面垂直,将“无数条”改为“所有”才正确;故①错误;
②垂直于这条直线的直线与这个平面可以是任何的位置关系,有可能是平行、相交、线在面内,故②错误.
③若a∥α,b⊥α,则根据线面平行、垂直的性质,必有a⊥b,正确;
④若a⊥b,则过b有且只有一个平面与a垂直,显然正确.
故答案为③④.
点评 本题考查空间的线面位置关系,考查空间想象能力和逻辑推理能力.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
5.若椭圆$\frac{y^2}{16}+\frac{x^2}{9}=1和双曲线\frac{y^2}{4}-\frac{x^2}{5}=1$的共同焦点为F1、F2,P是两曲线的一个交点,则|PF1|•|PF2|的值为( )
| A. | 12 | B. | 14 | C. | 3 | D. | 21 |
10.已知向量$\overrightarrow{a}$=(x,$\sqrt{3}$),$\overrightarrow{b}$=(x,-$\sqrt{3}$),若(2$\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
20.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(-$\frac{π}{6}$)的值为( )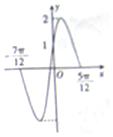

| A. | -1 | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
19.已知三棱柱ABC-A1B1C1的侧棱与底面垂直,体积为$\frac{9}{4}$,底面是边长为$\sqrt{3}$的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
20.已知tanα=-$\frac{3}{4}$,tan(π-β)=$\frac{1}{2}$,则tan(α-β)的值为( )
| A. | -$\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | -$\frac{11}{2}$ |