题目内容
设函数f(x)=
则f(-log32)= ;若f(f(t))∈[0,1],则实数t的取值范围是 .
|
考点:分段函数的应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:由-1≤-log32≤1,代入第一个解析式,计算即可得到f(-log32);通过t的范围,求出f(t)的表达式,判断f(t)的范围,然后代入已知函数,通过函数的值域求出t的范围即可.
解答:
解:由-1≤-log32≤1,则f(-log32)=3-log32=3log3
=
,
当t∈[-1,1],所以f(t)=3t∈[
,3],
又函数f(x)=
则f(f(t))=3(不成立)或f(f(t)=
-
•3t,
因为f(f(t))∈[0,1],
所以0≤
-
•3t≤1,即
≤3t≤3,
解得:log3
≤t≤1,又t∈[-1,1],
由于t=1,f(1)=3,f(f(1))不成立,
则实数t的取值范围[log3
,1);
当1<t<3时,f(t)=
-
•t∈(0,3),
由于f(f(t))∈[0,1],
即有0≤3
-
t≤1或0≤
-
•(
-
t)≤1,
解得t∈∅或1≤t≤
.
即有t的取值范围为(1,
].
综上可得t的范围是[log3
,1)∪(1,
].
故答案为:
,[log3
,1)∪(1,
].
| 1 |
| 2 |
| 1 |
| 2 |
当t∈[-1,1],所以f(t)=3t∈[
| 1 |
| 3 |
又函数f(x)=
|
则f(f(t))=3(不成立)或f(f(t)=
| 9 |
| 2 |
| 3 |
| 2 |
因为f(f(t))∈[0,1],
所以0≤
| 9 |
| 2 |
| 3 |
| 2 |
| 7 |
| 3 |
解得:log3
| 7 |
| 3 |
由于t=1,f(1)=3,f(f(1))不成立,
则实数t的取值范围[log3
| 7 |
| 3 |
当1<t<3时,f(t)=
| 9 |
| 2 |
| 3 |
| 2 |
由于f(f(t))∈[0,1],
即有0≤3
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
解得t∈∅或1≤t≤
| 13 |
| 9 |
即有t的取值范围为(1,
| 13 |
| 9 |
综上可得t的范围是[log3
| 7 |
| 3 |
| 13 |
| 9 |
故答案为:
| 1 |
| 2 |
| 7 |
| 3 |
| 13 |
| 9 |
点评:本题考查分段函数的综合应用,指数与对数不等式的解法,函数的定义域与函数的值域,函数值的求法,考查计算能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
设函数f(x)=
x3-ax2-ax,g(x)=2x2+4x+c
(1)试判断f(x)的零点个数;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
| 1 |
| 3 |
(1)试判断f(x)的零点个数;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
程序框图如图,如果程序运行的结果为s=132,那么判断框中可填入( )


| A、k≤10 | B、k≥10 |
| C、k≤11 | D、k≥11 |
 如图,圆O的弦AB、CD相交于点P,若AC=AD=2,PB=3,则AB=
如图,圆O的弦AB、CD相交于点P,若AC=AD=2,PB=3,则AB=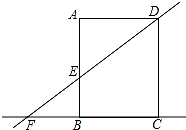 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.