题目内容
17.设函数f(x)=1-|2x-m|,x∈[0,1].若函数f(x)图象关于直线x=$\frac{1}{2}$对称,求曲线段y=f(f(x))的长度为$\sqrt{17}$.分析 利用函数的对称性求出m,然后化简函数的解析式求解即可.
解答 解:函数f(x)=1-|2x-m|,x∈[0,1].若函数f(x)图象关于直线x=$\frac{1}{2}$对称,
可知函数在x=$\frac{1}{2}$时,函数取得最大值.可得1-m=0,m=1,
函数f(x)=1-|2x-1|,x∈[0,1].
f(x)=$\left\{\begin{array}{l}{2x,x∈[0,\frac{1}{2})}\\{2-2x,x∈[\frac{1}{2},1]}\end{array}\right.$,
y=f(f(x))=$\left\{\begin{array}{l}{4x,x∈[0,\frac{1}{4})}\\{4-4x,x∈[\frac{3}{4},1]}\\{2-4x,x∈[\frac{1}{4},\frac{1}{2})}\\{4x-2,x∈[\frac{1}{2},\frac{3}{4})}\end{array}\right.$,
曲线段y=f(f(x))的长度为:4×$\sqrt{(\frac{1}{4})^{2}+{1}^{2}}$=$\sqrt{17}$.
点评 本题考查函数的解析式的求法,函数的图象的应用,考查分析问题解决问题的能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
5.函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数的解析式可以是( )
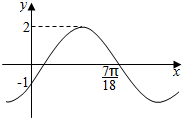

| A. | f(x)=2cos(3x+$\frac{2π}{3}$) | B. | f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) | ||
| C. | f(x)=2sin(3x-$\frac{π}{6}$) | D. | f(x)=2sin(3x-$\frac{π}{6}$)或f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) |
12.若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夹角为$\frac{π}{3}$的两个单位向量,则$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$;$\overrightarrow{b}$=-3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
2.设f(x)=x+sinx(x∈R),则下列说法错误的是( )
| A. | f(x)是奇函数 | B. | f(x)在R上单调递增 | C. | f(x)的值域为R | D. | f(x)是周期函数 |
9.已知集合A={x|x2-x-6>0),B={x|-1≤x≤4),则A∩B=( )
| A. | [-l,3) | B. | (3,4] | C. | [-1,2) | D. | (2,4] |
6.某学校共有3125名学生,一次活动中全体学生被排成一个n排的等腰梯形阵,且这n排学生数按每排都比前一排
多一人的规律排列,则当n取到最大值时,排在这等腰梯形阵最外面的一周的学生总人数是( )
多一人的规律排列,则当n取到最大值时,排在这等腰梯形阵最外面的一周的学生总人数是( )
| A. | 296 | B. | 221 | C. | 225 | D. | 641 |
7.已知函数f(x)=2sin2(ωx+$\frac{π}{6}$)(ω>0)在区间[$\frac{π}{6}$,$\frac{2π}{3}$]内单调递增,则ω的最大值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
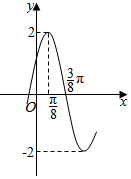 函数f(x)=2sin(ωx+φ),(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,求ω,φ的值.
函数f(x)=2sin(ωx+φ),(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,求ω,φ的值.