题目内容
5.函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数的解析式可以是( )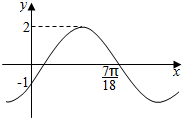
| A. | f(x)=2cos(3x+$\frac{2π}{3}$) | B. | f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) | ||
| C. | f(x)=2sin(3x-$\frac{π}{6}$) | D. | f(x)=2sin(3x-$\frac{π}{6}$)或f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) |
分析 由图形可以求出A,根据图象过(0,-1),($\frac{7π}{18}$,0),把点的坐标代入求出ω,φ,从而可得函数解析式.
解答 解:由图象知A=2,点(0,-1),($\frac{7π}{18}$,0)在函数图象上,
∵2sinφ=-1,
∴可得sinφ=-$\frac{1}{2}$,可得:φ=2kπ+$\frac{7π}{6}$,或φ=2kπ+$\frac{11π}{6}$,k∈Z
∵2sin($\frac{7π}{18}$ω+2kπ+$\frac{7π}{6}$)=0,或2sin($\frac{7π}{18}$ω+2kπ+$\frac{11π}{6}$)=0,
∴$\frac{7π}{18}$ω+$\frac{7π}{6}$=kπ,k∈Z,或$\frac{7π}{18}$ω+$\frac{11π}{6}$=kπ,k∈Z,
解得:ω=$\frac{18k}{7}$-3,或ω=$\frac{18k}{7}$-$\frac{33}{7}$,k∈Z,
∴当k=2,ω=$\frac{15}{7}$,φ=4π+$\frac{7π}{6}$,可得函数的解析式可以是f(x)=2sin($\frac{15}{7}$x+4π+$\frac{7π}{6}$)=2sin($\frac{15}{7}x-\frac{5π}{6}$).
当k=3,ω=3,φ=6π+$\frac{11π}{6}$,可得函数的解析式可以是f(x)=2sin(3x-$\frac{π}{6}$).
故选:D.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查分析问题解决问题的能力,解题的关键是初相的求法要注意,属于中档题.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
13.下列函数是偶函数,且最小正周期为π的是( )
| A. | y=sin(π-2x) | B. | y=sin2xcos2x | C. | y=cos22x+1 | D. | y=cos(2x-π) |
14.函数$f(x)=sin({ωx+\frac{π}{6}})({ω>0})$的最小正周期为π,则f(x)的单调递增区间可以是( )
| A. | $({-\frac{π}{3},\frac{π}{6}})$ | B. | $({-\frac{π}{12},\frac{5π}{12}})$ | C. | $({\frac{5π}{12},\frac{11π}{12}})$ | D. | $({\frac{π}{6},\frac{2π}{3}})$ |
15.如果一个函数f(x)在定义域D中满足:(1)任意x1,x2∈D,f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$;(2)存在x1,x2∈D,且x1≠x2,使得f(x1)=f(x2),则f(x)可以是( )
| A. | f(x)=x2+2x | B. | f(x)=cosx | C. | f(x)=2x-1 | D. | f(x)=$\frac{1}{2}$(ex-e-x) |