题目内容
下列结论中正确的是（ ）
A、lgx+
| ||||||
B、
| ||||||
C、sin2x+
| ||||||
D、当0＜x≤2时，x-
|
考点：基本不等式
专题：不等式的解法及应用
分析：A．当0＜x＜1时，lgx＜0，因此lgx+
的最小值不可能为2；
B．利用基本不等式性质即可得出；
C.sin2x+
＞2
=4，其最小值不可能为4；
D．当0＜x≤2时，令f（x）=x-
，利用导数研究其单调性极值最值即可得出．
| 1 |
| lgx |
B．利用基本不等式性质即可得出；
C.sin2x+
| 4 |
| sin2x |
sin2x•
|
D．当0＜x≤2时，令f（x）=x-
| 1 |
| x |
解答：
解：A．当0＜x＜1时，lgx＜0，因此lgx+
的最小值为2不正确；
B.
+
≥2
=2，当且仅当x=1时取等号，正确；
C.sin2x+
＞2
=4，其最小值不可能为4；
D．当0＜x≤2时，令f（x）=x-
，f′（x）=1+
＞0，∴函数f（x）在（0，2]上单调递增，当x=2时取得最大值
，因此不正确．
综上可知：只有B正确．
故选：B．
| 1 |
| lgx |
B.
| x |
| 1 | ||
|
|
C.sin2x+
| 4 |
| sin2x |
sin2x•
|
D．当0＜x≤2时，令f（x）=x-
| 1 |
| x |
| 1 |
| x2 |
| 3 |
| 2 |
综上可知：只有B正确．
故选：B．
点评：本题考查了基本不等式的性质、利用导数研究其单调性极值最值，考查了推理能力和计算能力，属于基础题．
练习册系列答案
相关题目
在复平面内，复数
+（1+i）2对应的点位于（ ）
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
满足a∈A且4-a∈A，a∈N且4-a∈N，有且只有2个元素的集合A的个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
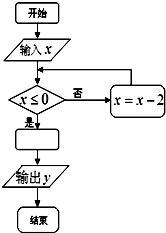如图是一个算法程序框图，当输入的x值为3时，输出的结果恰好是| 1 |
| 3 |
A、y=x -
| ||
B、y=x
| ||
| C、y=3-x | ||
| D、y=3x |
“α=β+2kπ（k∈Z）”是“tanα=tanβ”的（ ）条件．
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分又不必要 |
如果复数（1+bi）（2+i）是纯虚数，则|
|的值为（ ）
| 2b+3i |
| 1+bi |
| A、2 | ||
B、
| ||
| C、5 | ||
| D、15 |
不等式
＜0的解集是（ ）
| x(x-1)2 |
| x+1 |
| A、{x|-1＜x＜1} |
| B、{x|0＜x＜1} |
| C、{-1＜x＜0} |
| D、{x|x＞1或-1＜x＜0} |