题目内容
函数y=cos（
-x）的单调递增区间为 ．
| π |
| 4 |
考点：余弦函数的单调性
专题：计算题,三角函数的图像与性质
分析：利用余弦的诱导公式可将y=cos（
-x）转化为y=cos（x-
），再利用余弦函数的单调性即可求得函数y=cos（
-x）的单调递增区间．
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答：
解：∵y=cos（
-x）=cos（x-
），
由2kπ-π≤x-
≤2kπ，k∈Z得：
2kπ-
≤x≤2kπ+
，k∈Z．
∴原函数的单调递增区间为[2kπ-
，2kπ+
]（k∈Z）．
故答案为：[2kπ-
，2kπ+
]（k∈Z）．
| π |
| 4 |
| π |
| 4 |
由2kπ-π≤x-
| π |
| 4 |
2kπ-
| 3π |
| 4 |
| π |
| 4 |
∴原函数的单调递增区间为[2kπ-
| 3π |
| 4 |
| π |
| 4 |
故答案为：[2kπ-
| 3π |
| 4 |
| π |
| 4 |
点评：本题考查复合三角函数的单调性，着重考查余弦函数的诱导公式与单调性，属于基本知识的考查．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
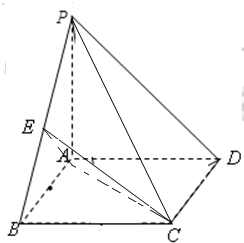如图，在四棱锥P-ABCD中，底面ABCD为矩形，侧棱PA⊥底面，且AB=2，BC=1，PA=2，E为PD的中点．