题目内容
15.已知函数f(x)=cos($\frac{π}{2}$+x)+sin2($\frac{π}{2}$+x),x∈R,则f(x)的最大值为( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
分析 利用诱导公式得到:f(x)=(sinx-$\frac{1}{2}$)2+$\frac{5}{4}$.根据二次函数和三角函数的单调性即可得出.
解答 解:f(x)=cos($\frac{π}{2}$+x)+sin2($\frac{π}{2}$+x)
=-sinx+cos2x
=-sinx+1-sin2x
=-(sinx-$\frac{1}{2}$)2+$\frac{5}{4}$.
∵x∈R,
∴当sinx=$\frac{1}{2}$,f(x)max=$\frac{5}{4}$.
故选:B.
点评 本题考查了诱导公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
3.方程x2+y2+4kx-2y+5k=0表示圆,则k的取值范围是( )
| A. | k>1 | B. | k>1或k<$\frac{1}{4}$ | C. | k<$\frac{1}{4}$ | D. | 以上答案 都不对 |
10.随机变量ξ的分布列为:
随机变量ξ的方差D(ξ)1.
| ξ | 0 | 1 | 2 | 3 |
| P | x | 0.2 | 0.3 | 0.4 |
7.函数f(x)=x3+ax2+3x-1在x=-3时取得极值,则a=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
4.有6个座位连成一片排,现有3人入座,则恰有两个空位相邻的不同坐法的种数是( )
| A. | 36 | B. | 48 | C. | 72 | D. | 120 |
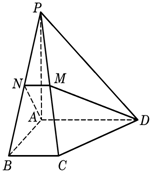 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.