题目内容
6.已知焦点在x轴上的椭圆C为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1,F1、F2分别是椭圆C的左、右焦点,离心率e=$\frac{\sqrt{2}}{2}$.(1)求椭圆C的方程;
(2)设点Q的坐标为(1,0),椭圆上是否存在一点P,使得直线PF1,PF2都与以Q为圆心的一个圆相切?若存在,求出P点坐标及圆的方程;若不存在,请说明理由.
分析 (1)椭圆C为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1焦点在x轴上,a=2$\sqrt{2}$,椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,解得:c=2.则b2=a2-c2=4即可求得椭圆C的方程;
(2)假设存在满足条件的点P,设出其坐标,根据两点式写出直线PF1,PF2的方程,根据圆的切线满足圆心到直线的距离等于半径,利用点到直线的距离公式列出有关点P的坐标的方程,再利用点P的坐标满足椭圆的方程,解方程组求得点P的坐标.
解答 解:(1)由题可知:椭圆C为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1焦点在x轴上,a=2$\sqrt{2}$,
椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,解得:c=2.
∴b2=a2-c2=4.
故椭圆C的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;…(4分)
(2)假设椭圆上存在一点P(x0,y0),
使得直线PF1,PF2都与以Q为圆心的一个圆相切,则Q到直线PF1,PF2的距离相等.
∵F1(-2,0),F2(2,0),
∴直线PF1的方程为(x0+2)y-y0x-2y0=0,
直线PF2的方程为(x0-2)y-y0x+2y0=0.…(6分)
∴d1=$\frac{丨{y}_{0}丨}{\sqrt{({x}_{0}-2)^{2}+{y}_{0}^{2}}}$=$\frac{丨3{y}_{0}丨}{\sqrt{({x}_{0}+2)^{2}+{y}_{0}^{2}}}$=d2,
化简整理得:8x02-40x0+32+8y02=0.…(9分)
∵点在椭圆上,
∴x02+2y02=8
由以上两式解得:x0=2或x0=8(舍去),
∴y0=$\sqrt{2}$或y0=-$\sqrt{2}$,此时相切的圆的半径r=1.…(11分)
∴椭圆上存在点P,其坐标为(2,$\sqrt{2}$)或(2,-$\sqrt{2}$),
使得直线PF1,PF2都与以Q为圆心的圆(x-1)2+y2=1相切.…(12分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查点到直线的距离公式,考查计算能力,属于中档题.

| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | 1 |
| A. | 钝角 | B. | 直角 | C. | 锐角 | D. | 60° |
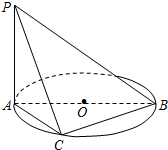 已知PA垂直于以AB为直径的ΘO所在的平面,C是ΘO上异于A,B的动点,PA=1,AB=2,当三棱锥P-ABC取得最大体积时,求:
已知PA垂直于以AB为直径的ΘO所在的平面,C是ΘO上异于A,B的动点,PA=1,AB=2,当三棱锥P-ABC取得最大体积时,求:(1)PC与AB所成角的大小;
(2)PA与面PCB所成角的大小.
| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
 已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,且二面角D-AE-C的正切值为-2.
已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,且二面角D-AE-C的正切值为-2. ,则
,则 ( )
( ) B.
B.
 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.