题目内容
18.在区间[0,2]上任取两个实数a,b,则函数f(x)=x3+ax-b在区间[-1,1]上有且只有一个零点的概率是$\frac{7}{8}$.分析 根据所给的条件很容易做出试验发生包含的事件对应的面积,而满足条件的事件是函数f(x)=x3+ax-b在区间[-1,1]上有且仅有一个零点,求出导函数,看出函数是一个增函数,有零点等价于在自变量区间的两个端点处函数值符号相反,得到条件,做出面积,根据几何概型概率公式得到结果.
解答  解:由题意知本题是一个几何概型,
解:由题意知本题是一个几何概型,
∵a∈[0,2],
∴f'(x)=3x2+a≥0
∴f(x)是增函数,
若f(x)在[-1,1]有且仅有一个零点,
则f(-1)•f(1)≤0
∴(-1-a-b)(1+a-b)≤0,
即(1+a+b)(1+a-b)≥0,
由线性规划内容知全部事件的面积为2×2=4,满足条件的面积4-$\frac{1}{2}×1×1$=$\frac{7}{2}$,
∴P=$\frac{\frac{7}{2}}{4}$=$\frac{7}{8}$,
故答案为:$\frac{7}{8}$.
点评 本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
相关题目
8.甲乙丙三人站成一排,则甲丙不相邻的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
9.已知对任意的实数m,直线x+y+m=0都不与曲线f(x)=x3-3ax(a∈R)相切.则实数a的取值范围为( )
| A. | $(-∞,-\frac{1}{3})$ | B. | $(-\frac{1}{3},+∞)$ | C. | $(\frac{1}{3},+∞)$ | D. | $(-∞,\frac{1}{3})$ |
6.已知某随机变量X的概率密度函数P(x)满足P(x)=P(-x),当x≤0时,$P(x)=\frac{1}{2}{e^x}$,则随机变量X落在区间(-1,1)内的概率为( )
| A. | $1-\frac{1}{e}$ | B. | $\frac{e+1}{e^2}$ | C. | $\frac{1}{e}$ | D. | $\frac{e-1}{e^2}$ |
13.定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,4)时,f(x)=(1og2015888)x-2,f(sin1)与f(cos1)的大小关系为( )
| A. | f(sin1)<f(cos1) | B. | f(sin1)=f(cos1) | C. | f(sin1)>f(cos1) | D. | 不确定 |
3.若全集U=R,集合A={x|x2-x-2≥0},B={x|log3(2-x)≤1},则A∩(∁UB)=( )
| A. | {x|x<2} | B. | {x|x<-1或x≥2} | C. | {x|x≥2} | D. | {x|x≤-1或x>2} |
7.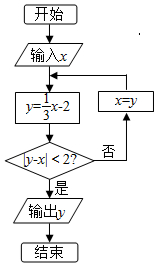 执行如图所示的程序框图,若输入x=9,则输出的y的值为( )
执行如图所示的程序框图,若输入x=9,则输出的y的值为( )
 执行如图所示的程序框图,若输入x=9,则输出的y的值为( )
执行如图所示的程序框图,若输入x=9,则输出的y的值为( )| A. | -$\frac{23}{9}$ | B. | 1 | C. | $\frac{8}{9}$ | D. | -$\frac{5}{3}$ |
8.若x轴上一点A与点B(3,12)的距离等于13,则点A的坐标是( )
| A. | (-2,0)或(5,0) | B. | (8,9)或(10,0) | C. | (-2,0)或(8,0) | D. | (0,0)或(10,0) |