题目内容
10.星城投公司到当地“美丽中国”旅行社统计了100名来到该市旅游的旅客的去处,发现游览科技馆,博物馆、海底世界三个景点的人数依次为40,50,60人,且客人是否游览哪个景点互不影响,如果用频率作为概率,Y表示旅客离开该市时游览的景点数和没有游览的景点数之差的绝对值.(Ⅰ)求Y的分布列及数学期望;
(Ⅱ)记“函数f(x)=x2-3Yx+1在区间[2,+∞)上单调递增”为事件A,试求事件A的概率.
分析 (1)分别记“客人游览科技馆”、“客人游览博物馆”、“客人游览海底世界”为事件A1、A2、A3,由已知A1,A2,A3相互独立,由题意Y的可能取值为1,3,分别求出相应的概率,由此能求出Y的分布列及数学期望.
(Ⅱ)要使f(x)在[2,+∞)上单调递增,当且仅不$\frac{3}{2}Y≤2$,即Y$≤\frac{4}{3}$,由此能求出事件A的概率.
解答 解:(1)∵星城投公司到当地“美丽中国”旅行社统计了100名来到该市旅游的旅客的去处,发现游览科技馆,博物馆、海底世界三个景点的人数依次为40,50,60人,
分别记“客人游览科技馆”、“客人游览博物馆”、“客人游览海底世界”为事件A1、A2、A3,由已知A1,A2,A3相互独立,
P(A1)=0.4,P(A2)=0.5,P(A3)=0.6,
Y表示旅客离开该市时游览的景点数和没有游览的景点数之差的绝对值,
∴Y的可能取值为1,3,
P(Y=3)=P(A1A2A3)+P($\overline{{A}_{1}}\overline{{A}_{2}}\overline{{A}_{3}}$)=2×0.4×0.5×0.6=0.24,
P(Y=1)=1-0.24=0.76,
∴Y的分布列为:
| Y | 1 | 2 |
| P | 0.76 | 0.24 |
(Ⅱ)∵函数f(x)=x2-3Yx+1=(x-$\frac{3}{2}Y$)2+1-$\frac{9}{4}{Y}^{2}$,
∴f(x)=x2-3Yx+1在区间[$\frac{3}{2}Y,+∞$)上单调递增,
要使f(x)在[2,+∞)上单调递增,当且仅不$\frac{3}{2}Y≤2$,即Y$≤\frac{4}{3}$,
∴事件A的概率P(A)=P(Y$≤\frac{4}{3}$)=P(Y=1)=0.76.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
20.某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些这些学生的原始成绩均分布在[50,100]内,发布成绩使用等级制,各等级划分标准见表,规定:A,B,C三级为合格等级,D为不合格等级.
为了解该校高一年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.
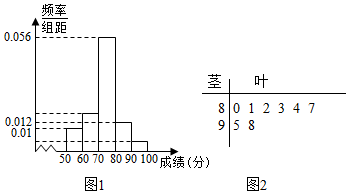
(1)求n和频率分布直方图中的x,y的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生中任选3人,求至少有1人成绩是合格等级的概率;
(3)在选取的样本中,从A,C两个等级的学生中随机抽取了3名学生进行调研,记ξ表示抽取的3名学生中为C等级的学生人数,求随机变量ξ的分布列及数学期望.
| 百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |

(1)求n和频率分布直方图中的x,y的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生中任选3人,求至少有1人成绩是合格等级的概率;
(3)在选取的样本中,从A,C两个等级的学生中随机抽取了3名学生进行调研,记ξ表示抽取的3名学生中为C等级的学生人数,求随机变量ξ的分布列及数学期望.
15.2015年9月12日青岛2015世界休闲体育大会隆重开幕.为普及体育知识,某校学生社团组织了14人进行“体育知识竞赛”活动,每人回答3个问题,答对题目个数及对应人数统计结果见表:
根据表格信息解答以下问题:
(Ⅰ)从14人中任选3人,求3人答对题目个数之和为6的概率;
(Ⅱ)从14人中任选2人,用X表示这2人答对题目个数之和,求随机变量X的分布列和数学期望EX.
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 3 | 2 | 5 | 4 |
(Ⅰ)从14人中任选3人,求3人答对题目个数之和为6的概率;
(Ⅱ)从14人中任选2人,用X表示这2人答对题目个数之和,求随机变量X的分布列和数学期望EX.
2.我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数如下表.
(Ⅰ)由以上统计数据估算月收入高于5500的调查对象中,持反对态度的概率;
(Ⅱ)若对月收入在[1500,2500),[2500,3500)的被调查对象中各随机选取两人进行跟踪调查,记选中的4人中赞成“延迟退休年龄”的人数为ξ,求随机变量ξ的分布列和数学期望.
| 月收入(元) | [1500,2500) | [2500,3500) | [3500,4500) | [4500,5500) | [5500,6500) | [6500,7500) |
| 频数 | 5 | 10 | 14 | 11 | 6 | 4 |
| 反对人数 | 4 | 8 | 11 | 6 | 2 | 1 |
(Ⅱ)若对月收入在[1500,2500),[2500,3500)的被调查对象中各随机选取两人进行跟踪调查,记选中的4人中赞成“延迟退休年龄”的人数为ξ,求随机变量ξ的分布列和数学期望.
19.设全集U=R,集合A={x|x≥2},B={x|0≤x<5},则集合A∩B=( )
| A. | {x|0≤x} | B. | {x|0<x≤2} | C. | {x|0≤x<2} | D. | {x|2≤x<5} |