题目内容
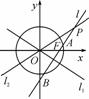
抛物线y2=2px的准线方程为x=-2,该抛物线上的每个点到准线x=-2的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线l1:y=x和l2:y=-x 相切的圆,
(1) 求定点N的坐标;
(2) 是否存在一条直线l同时满足下列条件:
① l分别与直线l1和l2交于A、B两点,且AB中点为E(4,1);
② l被圆N截得的弦长为2.
解:(1) 因为抛物线y2=2px的准线方程为x=-2.所以p=4,根据抛物线的定义可知点N是抛物线的焦点,所以定点N的坐标为(2,0).
(2) 假设存在直线l满足两个条件,显然l斜率存在,设l的方程为y-1=k(x-4),k≠±1.以N为圆心,同时与直线l1:y=x和l2:y=-x 相切的圆N的半径为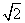 .因为l被圆N截得的弦长为2,所以圆心到直线的距离等于1, 即d=
.因为l被圆N截得的弦长为2,所以圆心到直线的距离等于1, 即d=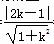 =1,解得k=0或
=1,解得k=0或 ,当k=0时,显然不合AB中点为E(4,1)的条件,矛盾, 当k=
,当k=0时,显然不合AB中点为E(4,1)的条件,矛盾, 当k= 时,l的方程为4x-3y-13=0.由
时,l的方程为4x-3y-13=0.由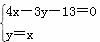 ,解得点A的坐标为(13,13);由
,解得点A的坐标为(13,13);由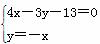 ,解得点B的坐标为
,解得点B的坐标为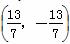 .显然AB中点不是E(4,1),矛盾,所以不存在满足条件的直线l.
.显然AB中点不是E(4,1),矛盾,所以不存在满足条件的直线l.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 ,则sinθ=____________,tanθ=____________.
,则sinθ=____________,tanθ=____________. +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为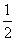 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为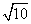 .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
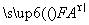 =λ
=λ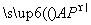 ,求λ的最大值.
,求λ的最大值.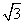 ,且其三个顶点均在抛物线E:x2=2py(p>0)上.
,且其三个顶点均在抛物线E:x2=2py(p>0)上.
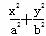 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为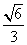 ,F为椭圆的右焦点,M、N两点在椭圆C上,且
,F为椭圆的右焦点,M、N两点在椭圆C上,且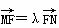 (λ>0),定点A(-4,0).
(λ>0),定点A(-4,0).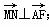
 ;
;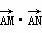 =
=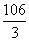 ,求椭圆C的方程.
,求椭圆C的方程. =1的右焦点为(3,0),则该双曲线的离心率为________.
=1的右焦点为(3,0),则该双曲线的离心率为________.