题目内容
已知椭圆C的方程为 +
+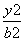 =1(a>b>0),双曲线
=1(a>b>0),双曲线 -
-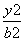 =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
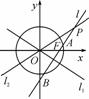
(1) 当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(2) 当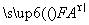 =λ
=λ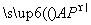 ,求λ的最大值.
,求λ的最大值.
解:(1) ∵双曲线的渐近线为y=± x,
x,
两渐近线夹角为60°,又 <1,
<1,
∴∠POx=30°,
即 =tan30°=
=tan30°= .
.
∴a=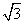 b.
b.
又a2+b2=4,∴a2=3,b2=1.
故椭圆C的方程为 +y2=1.
+y2=1.
(2) 由已知l:y= (x-c),与y=
(x-c),与y= x解得P
x解得P .
.
由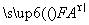 =λ
=λ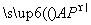 ,得A
,得A .
.
将A点坐标代入椭圆方程,
得(c2+λa2)2+λ2a4=(1+λ)2a2c2.
∴(e2+λ)2+λ2=e2(1+λ)2.
∴λ2= +3≤3-2
+3≤3-2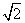 .
.
∴λ的最大值为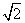 -1.
-1.

练习册系列答案
相关题目
 =
=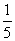 ,那么cosα=________.
,那么cosα=________.
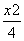 +y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
+y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点. ,求a;
,求a; =1表示椭圆,则k的取值范围是________.
=1表示椭圆,则k的取值范围是________.  -y2=1的一个焦点为(2,0),则它的离心率为________.
-y2=1的一个焦点为(2,0),则它的离心率为________.