题目内容
已知椭圆C：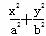
＝1(a＞b＞0)的离心率为
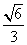，F为椭圆的右焦点，M、N两点在椭圆C上，且
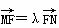(λ＞0)，定点A(－4，0)．
(1) 求证：当λ＝1时，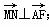
；
(2) 若当λ＝1时，有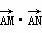
＝
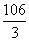，求椭圆C的方程．
(1) 证明：设M(x1，y1)，N(x2，y2)，F(c，0)，则
＝(c－x1，－y1)，
＝(x2－c，y2)．当λ＝1时，
，∴ －y1＝y2，x1＋x2＝2c.∵ M、N两点在椭圆C上，
(2) ∴
，∴ x
＝x
.若x1＝－x2，则x1＋x2＝0≠2c(舍去)，∴ x1＝x2，
(2) 解：当λ＝1时，由(1)知x1＝x2＝c，
代入(*)式得
c2＋8c＋16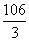＝，∴ c＝2或c＝－
(舍去)．∴ a2＝6，b2＝2，∴ 椭圆C的方程为
＝1.
练习册系列答案
相关题目
＝1表示椭圆，则k的取值范围是________. 
＝1(a＞b＞0)的左、右焦点，若在直线x＝
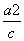上存在点P，使线段PF1的中垂线过点F2，则椭圆的离心率的取值范围是________．
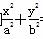＝1(a>b>0)，F1、F2分别为椭圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B.
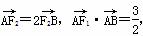，求椭圆的方程．
，左、右准线分别为l1：x＝－m－1，l2：x＝m＋1，且l1、l2分别与直线y＝x相交于A、B两点．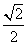
，求椭圆的方程；
<7时，求椭圆离心率的取值范围．
－y2＝1的一个焦点为(2，0)，则它的离心率为________．
的大小关系是______________．