题目内容
7.如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{2016}$的值的一个程序框图,则判断框内应填入的条件是( )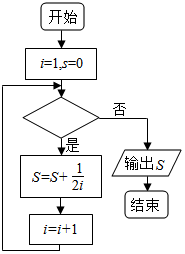
| A. | i≤1007 | B. | i≤1008 | C. | i>1008 | D. | i>1007 |
分析 由题意可知,首先是判断框中的条件满足,所以框图依次执行循环,框图执行第一次循环后,S的值为$\frac{1}{2}$,执行第二次循环后,s的值为$\frac{1}{2}+\frac{1}{4}$,满足$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{2016}$,框图应执行1008次循环,i的值为1009时判断框中的条件应该不满足,算法结束,由此得到判断框中的条件.
解答 解:执行程序框图,有s=0,
第1次循环:i=1,s=$\frac{1}{2}$,
第2次循环:i=2,s=$\frac{1}{2}+\frac{1}{4}$,
第3次循环:i=3,s=$\frac{1}{2}+\frac{1}{4}$+$\frac{1}{6}$,
…
第1008次循环:i=1008,s=$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{2016}$,
i=1009,不满足条件,退出循环,输出s的值,
则判断框内应填入的条件是:i≤1008或i<1009.
故选:B.
点评 本题考查了循环结构,是直到型循环,区别当型和直到型的关键在于是满足条件执行循环还是不满足条件执行循环,满足条件执行循环的是当型结构,不满足条件执行循环的是直到型结构,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.对于函数f(x),在使f(x)≥M成立的所有常数M中,我们把M的最大值称为f(x)的“下确界”,则函数f(x)=1-4x+$\frac{1}{5-4x}$,x∈(-∞,$\frac{5}{4}$)的“下确界“等于( )
| A. | -2 | B. | -4 | C. | -8 | D. | 不能确定 |
15.执行如图所示的程序框图,输出的结果为1538,则判断框内可填入的条件为( )


| A. | n>6? | B. | n>7? | C. | n>8? | D. | n>9? |
19.在如下程序框图中,已知f0(x)=sinx,则输出的结果是( )


| A. | sinx | B. | cosx | C. | -sinx | D. | -cosx |
16.A、B、C、D四名学生按任意次序站成一排,则A或B站在边上的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{2}$ |
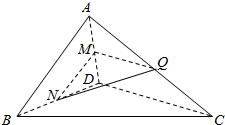 如图,在四面体ABCD中,AB⊥CD,AB⊥AD.M,N,Q分别为棱AD,BD,AC的中点.
如图,在四面体ABCD中,AB⊥CD,AB⊥AD.M,N,Q分别为棱AD,BD,AC的中点.