题目内容
18. 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.(1)画出偶函数f(x)的图象;并根据图象,写出f(x)的单调区间;同时写出函数的值域;
(2)求f(x)的解析式.
分析 (1)利用二次函数的性质以及函数的奇偶性画出函数的图象,写出单调区间以及函数的值域即可.
(2)利用函数的性质,转化求解函数的解析式即可.
解答 解:(1)图象如图所示: …(3分)
…(3分)
由图象得:函数f(x)的单调递减区间是(-∞,-1)和(0,1);
单调递增区间为(-1,0)和(1,+∞);…(4分)
函数的值域为[-1,+∞).…(5分)
(2)设x<0,则-x>0,
于是,f(-x)=(-x)2-2(-x)=x2+2x.…(7分)
又因为函数f(x)是偶函数,
所以f(x)=f(-x)=x2+2x.…(9分)
所以f(x)的解析式为:$f(x)=\left\{\begin{array}{l}{x^2}-2x\;,\;\;x≥0\;,\;\;\\{x^2}+2x\;,\;\;x<0\;.\;\end{array}\right.$…(10分)
点评 本题考查函数的图象的画法,函数的图象的应用,解析式的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
9.有下列命题:(1)若z是复数,则|z|2=z2;(2)任意两个复数不能比较大小;(3)b2-4ac>0时,一元二次方程ax2+bx+c=0(a,b,c∈C)有两个不等的实数根,其中所有错误命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
13.已知f(x)=ax3+bx+5,其中a,b为常数,若f(-9)=-7,则f(9)=( )
| A. | 17 | B. | 7 | C. | 16 | D. | 8 |
10.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则该三棱锥S-ABC的外接球的表面积为( )
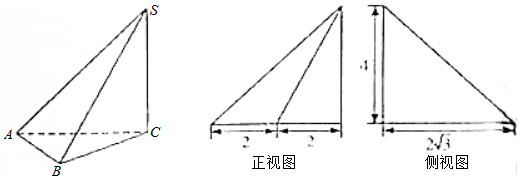

| A. | 32π | B. | $\frac{112π}{3}$ | C. | $\frac{28π}{3}$ | D. | $\frac{64}{3}$π |
7.已知函数f(x)=sin(2x+$\frac{π}{12}$),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
| A. | [$\frac{π}{12}$,$\frac{7π}{12}$] | B. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | C. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | D. | [-$\frac{π}{6}$,$\frac{5π}{6}$] |
8.执行如图所示的程序框图,若输出结果是5,则输入的整数p的可能性有( )


| A. | 6种 | B. | 7种 | C. | 8种 | D. | 9种 |