题目内容
圆x2+y2=4上到直线x+y-
=0的距离等于1的点有（ ）个．
| 2 |
| A、0 | B、1 | C、2 | D、3 |
考点：直线与圆的位置关系
专题：计算题,直线与圆
分析：求出圆心到直线的距离，与半径比较，即可得到距离等于1的点的个数．
解答：
解：圆x2+y2=4它是一个以（0，0）为圆心以2为半径的圆．
圆心到x+y-
=0的距离为d=
=1，
作与直线x+y-
=0距离为1的直线，会发现这样的直线有两条（一条在直线的上方，一条在直线的下方），上面的那条直线与圆有一个交点，下面的与圆有二个交点，所以圆上共有三个点与直线距离为1．
故选：D．
圆心到x+y-
| 2 |
|-
| ||
|
作与直线x+y-
| 2 |
故选：D．
点评：本题考查了直线与圆的位置关系，用到点到直线的距离公式，以及数形结合思想．
练习册系列答案
相关题目
已知双曲线
-
=1的一个焦点与抛物线y2=-4x的焦点重合，且双曲线的离心率为
，则此双曲线的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、5x2-
| ||||
B、5x2-
| ||||
C、
| ||||
D、
|
过原点的直线与圆x2+y2-4y+3=0相切，若切点在第二象限，则该直线的方程是（ ）
A、y=
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
【文科】如果双曲线的焦距等于两条准线间距离的4倍，则此双曲线的离心率为（ ）
| A、4 | ||
B、
| ||
C、
| ||
| D、2 |
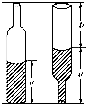如图，啤酒瓶的高为h，瓶内酒面高度为a，若将瓶盖盖好倒置，酒面高度为a′（a′+b=h），则酒瓶容积与瓶内酒的体积之比为（ ）A、1+
| ||
B、1+
| ||
C、1+
| ||
D、1+
|