题目内容
15.已知函数f(x)=sin($\frac{π}{2}$-x)sinx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$.(1)求f(x)的最小正周期;
(2)讨论f(x)在[$\frac{π}{6}$,$\frac{5π}{6}$]上的单调性,并求出在此区间上的最小值.
分析 (1)利用诱导公式和辅助角公式将已知函数解析式转化为正弦函数,根据正弦函数的性质来求最小正周期;
(2)根据自变量的取值范围来求正弦函数的值域.
解答 解:(1)f(x)=sin($\frac{π}{2}$-x)sinx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$
=cosxsinx+$\frac{\sqrt{3}(1-2co{s}^{2}x)}{2}$=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x=sin(2x-$\frac{π}{3}$),
属于T=π.
(2)当x∈[$\frac{π}{6}$,$\frac{5π}{6}$]时,2x-$\frac{π}{3}$∈[0,$\frac{4π}{3}$],令2x-$\frac{π}{3}$=$\frac{π}{2}$得x=$\frac{5π}{12}$,
所以f(x)在[$\frac{π}{6}$,$\frac{5π}{12}$]上单调递增,f(x)在[$\frac{5π}{12}$,$\frac{5π}{6}$]上单调递减,
所以f(x)min=f($\frac{5π}{6}$)=sin$\frac{4π}{3}$=-$\frac{\sqrt{3}}{2}$.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
相关题目
5.一台机器由于使用时间较长,但还可以使用,它按不同的转速生产出来的某机器零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,如表是抽样试验结果:
若实际生产中,允许每小时的产品中有缺点的零件数最多为10个,那么机器的转速应该控制所在的范围是( )
| 转速x/(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
| A. | 10转/s以下 | B. | 15转/s以下 | C. | 20转/s以下 | D. | 25转/s以下 |
20.已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩(∁UB)等于( )
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |
7.设A={x∈Z|x≤6},B={x∈Z|x>1},那么A∩B等于( )
| A. | {x|1<x≤6} | B. | {1,2,3,4,5,6} | C. | {2,3,4,5,6} | D. | {2,3,4,5} |
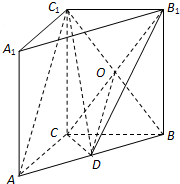 (理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.
(理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.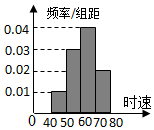 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论: