题目内容

3．设i是虚数单位，则复数z=$\frac{i-3}{1+i}$的实部为（　　）
A．2B．-2C．1D．-1

分析 直接利用复数代数形式的乘除运算化简得答案．

解答 解：∵z=$\frac{i-3}{1+i}$=$\frac{（i-3）（1-i）}{（1+i）（1-i）}=\frac{-2+4i}{2}=-1+2i$，
∴复数z=$\frac{i-3}{1+i}$的实部为-1．
故选：D．

点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础的计算题．

练习册系列答案
相关题目
13．已知函数f（x）=|x+1|-|x-1|．
（1）解关于x的不等式f（x）≤1；
（2）设函数f（x）的最大值为M，若M=3a+4b（a＞0，b＞0），求证：$\frac{1}{a+3b}+\frac{1}{2a+b}$≥2．
14．在一次共有15000名考生的某市高二的联考中，这些学生的数学成绩ξ服从正态分布 N（100，δ2），且p（80＜ξ≤100）=0.35．若按成绩分层抽样的方式抽取100份试卷进行分析，则应从120分以上的试卷中抽取（　　）
A．20份B．15份C．10份D．5份
11．已知直线l过点P（1，1），且与曲线y=x3在点P处的切线互相垂直，则直线l的方程为（　　）
A．x+3y+4=0B．x+3y-4=0C．3x-y+2=0D．3x-y-2=0
18．如图1，平面五边形ABCFE是由边长为2的正方形ABCD与上底为1，高为$\sqrt{3}$的直角梯形组合而成，将五边形ABCFE沿着CD折叠，得到图2所示的空间几何体，其中AF⊥CF．
（Ⅰ）证明：BD⊥平面AFC；
（Ⅱ）求二面角A-FB-C的正弦值．
8．已知复数z满足z•i=1+2i，则在复平面内，z所对应的点的坐标是（　　）
A．（2，1）B．（1，2）C．（-1，2）D．（2，-1）
15．如果{an}为递增数列，则{an}的通项公式可以是（　　）
A．an=-n+2（n∈N*）B．an=1+log3n（n∈N*）C．an=$\frac{1}{{2}^{n}}$（n∈N*）D．an=n2-3n（n∈N*）
12．已知$\overrightarrow{a}$=（m，1），$\overrightarrow{b}$=（1，-2）．若 $\overrightarrow{a}$∥$\overrightarrow{b}$，则实数m=-$\frac{1}{2}$；若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则实数 m=2；若|$\overrightarrow{a}$|＜|$\overrightarrow{b}$|，则实数m的取值范围是（-2，2），．
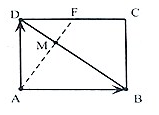13．如图，在矩形ABCD中，F是边CD的中点，M是AF与BD交点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$
（1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示向量$\overrightarrow{AF}$
（2）证明：M是对角线BD的三等分点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网