题目内容
2.已知以椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{m}$=1(m>0)的焦点连线F1F2为直径的圆和该椭圆在第一象限相交于点P.若△PF1F2的面积为1,则m的值为1.分析 由已知可得,|PF1|+|PF2|=4,|PF1|•|PF2|=2.然后结合勾股定理及椭圆定义列式求得m值.
解答 解:由题意,|PF1|+|PF2|=4,且$\frac{1}{2}$|PF1|•|PF2|=1,即|PF1|•|PF2|=2.
且$|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}$=$|{F}_{1}{F}_{2}{|}^{2}$=4(4-m),
则$(|P{F}_{1}|+|P{F}_{2}|)^{2}=16$,
即$|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}+2|P{F}_{1}|•|P{F}_{2}|=16$,
∴16-4m+2×2=16,解得m=1.
故答案为:1.
点评 本题考查椭圆的简单性质,考查了椭圆定义的应用,是基础的计算题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
10.设全集U=R,集合A={x|x2-1<0},B={x|x(x-3)>0}则A∩(∁UB)=( )
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|-1<x<0} |
17.经过点(-1,2)且与直线3x-5y+6=0垂直的直线的方程为( )
| A. | 3x-5y+13=0 | B. | 5x+3y-1=0 | C. | 5x+3y+1=0 | D. | 5x-3y+11=0 |
12.复数z满足z(1+i)=|1-i|,则复数z的虚部是( )
| A. | -1 | B. | 1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
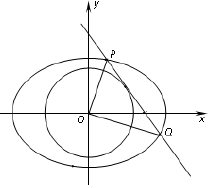 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,点(2,1)在椭圆C上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,点(2,1)在椭圆C上.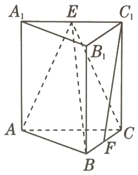 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.