题目内容

4．已知各项为整数的等差数列{an}的前n项和为Sn，a1为首项，公差为d，对任意n∈N*，当n≠6时，总有S6＞Sn，则a1的最小值是（　　）
A．9B．11C．15D．16

分析 由已知得该等差数列的前6项均为正数，从第7项开始是负数，由此能求出首项的最小值．

解答 解：∵各项为整数的等差数列{an}的前n项和为Sn，
a1为首项，公差为d，
对任意n∈N*，当n≠6时，总有S6＞Sn，
∴$\left\{\begin{array}{l}{{a}_{1}+5d＞0}\\{{a}_{1}+6d＜0}\\{d∈Z}\end{array}\right.$，
解得-5d＜a1＜-6d，
∵a1是整数，∴当d=-2时，a1取最小值11．
故选：B．

点评 本题考查等差数列的首项的最小值的求法，是中档题，解题时要认真审题，注意等差劲数列的性质的合理运用．

练习册系列答案
相关题目
14．已知a＞0，b＜0，且（4a-1）（2b+1）=-9，若（2a-b）x2-abx-6≥0总成立，则正实数x的取值范围是[1，+∞）．
15．已知数列{an}的前n项和为Sn，a1=$\frac{1}{2}$，Sn=n2an．
（1）分别计算a2，a3，a4，猜想通项公式an，并用数学归纳法证明之；
（2）求数列{an}的前n项和Sn．
12．已知0＜α＜$\frac{π}{2}$，tanα=$\frac{4}{3}$，tan（α-β）=-$\frac{1}{3}$，则tanβ=3；$\frac{cos2β•sinβ}{\sqrt{2}cos（β+\frac{π}{4}）}$=$\frac{6}{5}$．
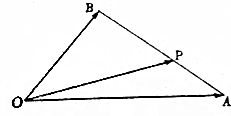19．如图，在△OAB中，已知P为线段AB上的一点．|$\overrightarrow{OA}$|=4，|$\overrightarrow{OB}$|=3，且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°．
（1）若$\overrightarrow{BP}$=3$\overrightarrow{PA}$，求$\overrightarrow{OP}$•$\overrightarrow{AB}$的值；
（2）若$\overrightarrow{BP}$=λ$\overrightarrow{PA}$，求当OP⊥AB时λ的值．
9．y=$\frac{1}{2}$sin（6x+1）的最大值（　　）
A．$\frac{1}{2}$B．-$\frac{1}{2}$C．6D．1
16．不等式$\frac{1}{1-x}$＜x+1的解集是{x|x＞1}．
13．已知{an}是等差数列且公差d＞0，a1=1且a2，a4，a8是等比数列．
（1）求{an}的通项公式；
（2）若数列{an}的前n项和为Sn，求数列{$\frac{1}{{S}_{n}}$}的前2016项和T2016．
14．求过点B（-5，4），且与直线2x-5y+2=0垂直的直线方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网