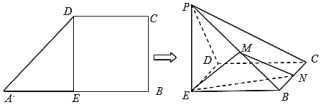
题目内容
【题目】已知函数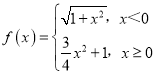 ,点
,点![]() 是函数
是函数![]() 图象上不同的两点,则
图象上不同的两点,则![]() 为坐标原点)的取值范围是( )
为坐标原点)的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据分段函数的表达式,分别求出对应切线和双曲线渐近线的倾斜角,结合位置关系判断∠AOB的大小即可.
当x<0时,y=![]() ,则y2=1+x2,当
,则y2=1+x2,当![]() 时,
时,![]() ,作出函数图象:
,作出函数图象:

当x<0时,y=![]() ,则y2=1+x2,
,则y2=1+x2,
即![]() ,为双曲线在第二象限的一部分,
,为双曲线在第二象限的一部分,
双曲线的渐近线方程为![]() ,
,
若B在双曲线上,则∠BOy的范围是0<∠BOy<![]() ,
,
设当x≥0时,过原点的切线与f(x)=![]() x2+1,相切,
x2+1,相切,
设切点为![]() ,
,
则f′(x)=![]() x,即切线斜率k=
x,即切线斜率k=![]() a,
a,
则切线方程为![]() ,
,
∵切线过原点,
∴![]() ,
,
即![]() ,
,
得![]()
![]() =1,即
=1,即![]() =
=![]() ,则
,则![]() =
=![]() ,
,
则切线斜率![]() ,即切线倾斜角为
,即切线倾斜角为![]() ,
,
则∠AOy的最大值为![]() ,
,
即0≤∠AOy≤![]() ,
,
则0<∠AOy+∠BOy<![]() ,
,
即0<∠AOB<![]() ,
,
故选:A.

练习册系列答案
相关题目
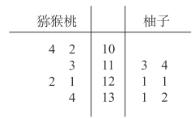
【题目】某歌手大赛进行电视直播,比赛现场有6名特约嘉宾给每位参赛选手评分,场内外的观众可以通过网络平台给每位参赛选手评分.某选手参加比赛后,现场嘉宾评分情况如下表;场内外共有数万名观众参与了评分,组织方将观众评分按照![]() ,
,![]() ,
,![]() 分组,绘成频率分布直方图如下:
分组,绘成频率分布直方图如下:
嘉宾 |
|
|
|
|
|
|
评分 | 96 | 95 | 96 | 89 | 97 | 98 |
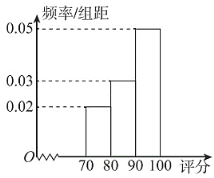
(1)从观众中任取三人,求这三人中恰有1人分数在![]() 另2人分数在
另2人分数在![]() 的概率;
的概率;
(2)从嘉宾中随机选3人,记3人中分数不低于96分的人数为![]() ,求
,求![]() 的期望;
的期望;
(3)嘉宾评分的平均数为![]() ,场内外的观众评分的平均数为
,场内外的观众评分的平均数为![]() 与
与![]() 的大小关系(不需要证明).
的大小关系(不需要证明).