Question

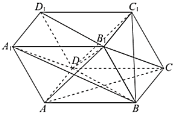
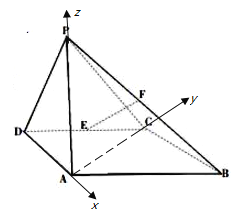
【题目】如图，在直角梯形中，，，，为的中点，沿将折起，使得点到点位置，且，为的中点，是上的动点（与点，不重合）.

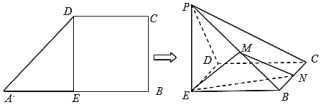
（Ⅰ）证明：平面平面垂直；

（Ⅱ）是否存在点，使得二面角的余弦值？若存在，确定点位置；若不存在，说明理由.

Answer 1

【答案】（Ⅰ）见解析 （Ⅱ）存在，此时为的中点.

【解析】

（Ⅰ）证明平面，得到平面平面，故平面平面，平面，得到答案.

（Ⅱ）假设存在点满足题意，过作于，平面，过作于，连接，则，过作于，连接，是二面角的平面角，设，，计算得到答案.

（Ⅰ）∵，，，∴平面.

又平面，∴平面平面，

而平面，，∴平面平面，

由，知，可知平面，

又平面，∴平面平面.

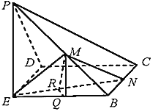
（Ⅱ）假设存在点满足题意，过作于，由知，

易证平面，所以平面，

过作于，连接，则（三垂线定理），

即是二面角的平面角，

不妨设，则，

在中，设（），由得，

即，得，∴，

依题意知，即，解得，

此时为的中点.

综上知，存在点，使得二面角的余弦值，此时为的中点.