题目内容
18.已知数列{an}满足${a_n}=({{n^2}+4n})cosnπ$,则{an}的前50项的和为1375.分析 由当n是奇数时,cosnπ=-1;当n是偶数时,cosnπ=1.an=(-1)n(n2+4n)=(-1)nn2+(-1)n×4n,S50=(-12+22-32+42-…+502)+4(-1+2-3+4-…+50),即可求得{an}的前50项的和.
解答 解:当n是奇数时,cosnπ=-1;当n是偶数时,cosnπ=1.
则an=(-1)n(n2+4n)=(-1)nn2+(-1)n×4n,
{an}的前50项的和S50=a1+a2+a3+…+a50,
=(-12+22-32+42-…+502)+4(-1+2-3+4-…+50),
=(1+2+3+4+…+50)+4×25,
=1275+100,
=1375,
故答案为:1375
点评 本题考查等差数列的性质,考查数列前n项和的求法,考查计算能力,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
9.已知f(x)=ax2+(b-a)x+c-b(其中a>b>c),若a+b+c=0,x1、x2为f(x)的两个零点,则|x1-x2|的取值范围为( )
| A. | ($\frac{3}{2}$,2$\sqrt{3}$) | B. | (2,2$\sqrt{3}$) | C. | (1,2) | D. | (1,2$\sqrt{3}$) |
6.已知x,y满足:$\left\{{\begin{array}{l}{x≥0}\\{x+y≤2}\\{x-y≤0}\end{array}}\right.$,若目标函数z=ax+y取最大值时的最优解有无数多个,则实数a的值是( )
| A. | 0 | B. | -1 | C. | ±1 | D. | 1 |
7.已知集合A={x|x>0},函数$f(x)=\sqrt{(2-x)(x-3)}$的定义域为集合B,则A∩B=( )
| A. | [3,+∞) | B. | [2,3] | C. | (0,2]∪[3,+∞) | D. | (0,2] |
8.复数${(1-i)^2}+\frac{2}{1-i}$的共轭复数是( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
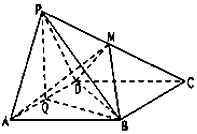 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.