题目内容
1．当k为何值时，关于x的不等式$\frac{2{x}^{2}+2kx+k}{4{x}^{2}+6x+3}$＜1的解集是R．分析 化简分式不等式为二次不等式，利用“三个二次”的关系即可解出．
解答 解：因为4x2+6x+3＞0恒成立，所以原不等式可化为2x2+2kx+k＞4x2+6x+3；
即：2x2+（6-2k）x+3-k＞0，
只需△=（6-2k）2-8（3-k）＜0，可得：k2-4k+3＜0，
解得1＜k＜3．
点评 本题考查函数的恒成立问题，考查转化思想，熟练掌握“三个二次”的关系是解题的关键．
练习册系列答案
相关题目
11．过点A（3，1）的直线l与圆C：x2+y2-4y-1=0相切于点B，则$\overrightarrow{CA}•\overrightarrow{CB}$=（ ）
| A． | 0 | B． | $\sqrt{5}$ | C． | 5 | D． | $\frac{{\sqrt{50}}}{3}$ |
12．
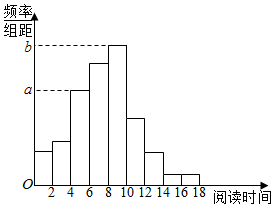从某校随机抽取200名学生，获得了他们的一周课外阅读时间（单位：小时）的数据，整理得到数据分组级频数分布直方图：
（1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；
（2）求频率分布直方图中的a，b的值；
（3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的200名学生该周课外阅读时间的平均数在第几组．
从某校随机抽取200名学生，获得了他们的一周课外阅读时间（单位：小时）的数据，整理得到数据分组级频数分布直方图：| 编号 | 分组 | 频数 |
| 1 | [0，2） | 12 |
| 2 | [2，4） | 16 |
| 3 | [4，6） | 34 |
| 4 | [6，8） | 44 |
| 5 | [8，10） | 50 |
| 6 | [10，12） | 24 |
| 7 | [12，14） | 12 |
| 8 | [14，16） | 4 |
| 9 | [16，18） | 4 |
| 合计 | 200 | |
（2）求频率分布直方图中的a，b的值；
（3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的200名学生该周课外阅读时间的平均数在第几组．
11．过原点的一条直线与双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）交于A，B两点，P为双曲线上不同于A，B的一个动点，且直线PA、PB的斜率之积为3，若抛物线C2：y2=2px（p＞0）的焦点到双曲线C1的渐近线的距离为2，则该抛物线C2的标准方程为（ ）
| A． | y2=$\frac{16\sqrt{3}}{3}$x | B． | y2=16x | C． | y2=$\frac{8\sqrt{3}}{3}$x | D． | y2=8x |