题目内容

一个正方体内接于一个球，过球心作一个截面，则截面不可能的图形为（　　）
A、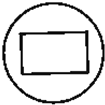
B、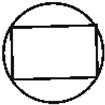
C、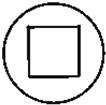
D、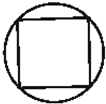
考点：平行投影及平行投影作图法,球内接多面体
专题：空间位置关系与距离
分析：当截面的角度和方向不同时，球的截面不相同，应分情况考虑即可．
解答： 解：当截面平行于正方体的一个侧面时得C，
当截面过正方体的体对角面时得B，
当截面不平行于任何侧面和对角面时得A，
但无论如何都不能截出D，
故选D．
点评：本题主要考查了球内接多面体、棱柱的结构特征．注意截面的形状既与被截的几何体有关，还与截面的角度和方向有关．
练习册系列答案
相关题目
关于三角函数f（x）=sin（x+
3
2
π）的图象，下列说法正确的是（　　）
A、f（x）是奇函数
B、f（x）的图象关于直线x=
π
2
对称
C、f（x）的周期为π
D、f（x）的图象关于点（
π
2
，0）对称
若存在实常数k和b，使得函数F（x）和G（x）对其公共定义域上的任意实数x都满足：F（x）≥kx+b和G（x）≤kx+b恒成立，则称此直线y=kx+b为F（x）和G（x）的“隔离直线”．已知函数f（x）=x2（x∈R），g（x）=
1
x
（x＜0），h（x）=2elnx．有下列命题：
①F（x）=f（x）-g（x）在x∈（-
1
32
，0）内单调递增；
②f（x）和g（x）之间存在“隔离直线”，且b的最小值为-4；
③f（x）和g（x）之间存在“隔离直线”，且k的取值范围是（-4，0]；
④f（x）和h（x）之间存在唯一的“隔离直线”y=2
e
x-e．
其中真命题的个数有（　　）
A、1个B、2个C、3个D、4个
（理）已知不等式（2a-b-c）（a-c）•2n≥（a-b）（b-c）（t•2n+1）对任意a＞b＞c及n∈N恒成立，则实数t的取值范围为 （　　）
A、（-∞，4
2
-1]
B、（-∞，2+2
2
]
C、[4
2
-1，+∞）
D、[2+2
2
，+∞）
当输入a的值为2，b的值为-3时，右边程序运行的结果是（　　）
A、-2B、-1C、1D、2
直线l的倾斜角为60°，则直线l的斜率是（　　）
A、
1
2
B、
3
2
C、-
3
D、
3
计算sin45°cos15°+cos45°sin15°=（　　）
A、-
3
2
B、-
1
2
C、
1
2
D、
3
2
命题“?x∈（0，+∞），x3-x2+1≥0，”的否定是（　　）
A、?x∈（0，+∞），x3-x2+1≤0
B、?x∈（0，+∞），x3-x2+1≤0
C、?x∈（0，+∞），x3-x2+1＜0
D、?x∈（0，-∞），x3-x2+1＜0
观察下面一组组合数等式：
1•
C
1
n
=n•
C
0
n-1
；
2•
C
2
n
=n•
C
1
n-1
；
3•
C
3
n
=n•
C
2
n-1

…
（Ⅰ）由以上规律，请写出第k（k∈N*）个等式并证明；
（Ⅱ）随机变量X～B（n，p），求证：EX=np．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网