题目内容

设（1+2x-3x2）n=a0+a1x+a2x2+…+a2nx2n（n∈N*）
（1）求a0；
（2）求a2（用n表示）
考点：二项式定理的应用
专题：计算题,二项式定理
分析：（1）令x=0，可得a0=1；
（2）（1+2x-3x2）n=（1+3x）n（1-x）n，利用二项式定理可得结论．
解答： 解：（1）令x=0，可得a0=1；
（2）（1+2x-3x2）n=（1+3x）n（1-x）n，
∴a2=
C
0
n
•30•
C
2
n
•（-1）2+
C
1
n
•3•
C
1
n
•(-1)+
C
2
n
•32•
C
0
n
•(-1)0=2n2-5n（n∈N*）．
点评：求二项展开式中的系数和问题，常采用的方法是赋值法．此法的关键是通过观察给未知数赋什么值能得到要求的系数和．
练习册系列答案
相关题目
观察下面一组组合数等式：
1•
C
1
n
=n•
C
0
n-1
；
2•
C
2
n
=n•
C
1
n-1
；
3•
C
3
n
=n•
C
2
n-1

…
（Ⅰ）由以上规律，请写出第k（k∈N*）个等式并证明；
（Ⅱ）随机变量X～B（n，p），求证：EX=np．
在三角形ABC中，（a+b+c）（b+c-a）=
6
bc，求cosA．
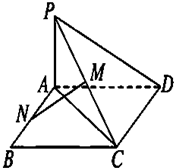如图四边形ABCD是矩形，PA⊥平面ABCD，PA=AD，M、N分别是PC、AB的中点．
?①求证MN∥平面PAD；
?②求证MN⊥平面PCD．
用五点法作出函数f（x）=3sin（
π
3
-2x）在一个周期内的图象（要求列表作图）．
已知椭圆的两个焦点坐标分别是（-2，0），（2，0），并且经过点（
5
2
，-
3
2
），求它的标准方程．
已知双曲线焦点在y轴上，F1，F2为其焦点，焦距为10，焦距是实轴长的2倍．求：
（1）双曲线的渐近线方程；
（2）若P为双曲线上一点，且满足∠F1PF2=60°，求△PF1F2的面积．
执行如图所示的流程图，输出的a的值为
 
．
为亮化美化城市，现在要把一条路上7盏路灯全部改成彩色路灯．如果彩色路灯有红黄与蓝三种颜色，在安装时要求相同颜色的路灯不能相邻，而且每种颜色的路灯至少2盏，有
 
种不同的安装方法．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网