题目内容
4.命题“?x∈R,x2-1>0”的否定是( )| A. | ?x∈R,x2-1≤0 | B. | ?x0∈R,x02-1>0 | C. | ?x0∈R,x02-1≤0 | D. | ?x∈R,x2-1<0 |
分析 根据全称命题的否定是特称命题进行判断即可.
解答 解:命题为全称命题,则命题的否定是特称命题,
即?x0∈R,x02-1≤0,
故选:C
点评 本题主要考查含有量词的命题的否定,比较基础.

练习册系列答案
相关题目
15.已知随机变量ξ服从正态分布N(2,σ2),且函数f(x)=x2+2x-ξ+1不存在零点的概率为0.08,则随机变量P(0<ξ<2)=( )
| A. | 0.08 | B. | 0.42 | C. | 0.84 | D. | 0.16 |
12.设点A(3,3,1),B(1,0,5),C(0,1,0),则线段AB的中点与点C的距离为( )
| A. | $\frac{\sqrt{13}}{4}$ | B. | $\frac{\sqrt{13}}{2}$ | C. | $\frac{\sqrt{53}}{4}$ | D. | $\frac{\sqrt{53}}{2}$ |
16.若函数y=f(x)的图象上存在关于原点对称的两点M,N,则称函数f(x)有一组“对点”(“M与N”和“N与M”视为同一组“对点”),已知f(x)=$\left\{\begin{array}{l}{2x^2+4x,x<0}\\{\frac{m}{e^x},x≥0}\end{array}\right.$,有两组“对点”,则非零实数m的取值范围是( )
| A. | ((4-4$\sqrt{2}$)•e${\;}^{-\sqrt{2}}$,0)∪(0,(4$\sqrt{2}$-4)•e${\;}^\sqrt{2}$) | B. | ((2-2$\sqrt{2}$)•e${\;}^{-\sqrt{2}}$,0)∪(0,(2$\sqrt{2}$-2)•e${\;}^\sqrt{2}$) | ||
| C. | (0,(2$\sqrt{2}$-2)•e${\;}^\sqrt{2}$) | D. | (0,(4$\sqrt{2}$-4)•e${\;}^\sqrt{2}$) |
13.已知集合A={x|x2-2x-3=0},B={x|-2<x<3},则A∩B=( )
| A. | {-1,3} | B. | {-1} | C. | {3} | D. | ∅ |
14.已知角α在第三象限,且cosα=-$\frac{4}{5}$,则sinα的值为( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
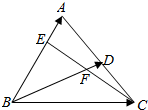 如图,在△ABC中,D为AC的中点,E是AB上的点,且$\frac{AE}{EB}$=$\frac{1}{2}$,CE和BD交于点F,设$\overrightarrow{BD}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.
如图,在△ABC中,D为AC的中点,E是AB上的点,且$\frac{AE}{EB}$=$\frac{1}{2}$,CE和BD交于点F,设$\overrightarrow{BD}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.