题目内容
已知函数f(x)= sin 2xsin φ+cos2xcos φ-
sin 2xsin φ+cos2xcos φ- sin(
sin(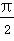 +φ)(0<φ<π),其图象过点
+φ)(0<φ<π),其图象过点
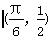 .
.
(1)求φ的值;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在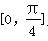 上的最大值和最小值.
上的最大值和最小值.
解 (1)因为f(x)= sin 2xsin φ+cos2xcos φ-
sin 2xsin φ+cos2xcos φ- sin(
sin(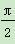 +φ)(0<φ<π),
+φ)(0<φ<π),
所以f(x)= sin 2xsin φ+
sin 2xsin φ+ cos φ-
cos φ- cos φ
cos φ
= sin 2xsin φ+
sin 2xsin φ+ cos 2xcos φ
cos 2xcos φ
= (sin 2xsin φ+cos 2xcos φ)
(sin 2xsin φ+cos 2xcos φ)
= cos(2x-φ).
cos(2x-φ).
又函数图象过点( ,
, ),
),
所以 =
= cos(2×
cos(2× -φ),
-φ),
即cos( -φ)=1,
-φ)=1,
又0<φ<π,所以φ= .
.
(2)由(1)知f(x)= cos(2x-
cos(2x- ),将函数y=f(x)的图象上各点的横坐标缩短到原来的
),将函数y=f(x)的图象上各点的横坐标缩短到原来的 ,
,
所以y=g(x)在[0,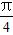 ]上的最大值和最小值分别为
]上的最大值和最小值分别为 和-
和- .
.

练习册系列答案
相关题目
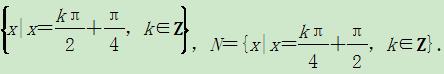 .则( )
.则( ) )=-
)=-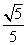 ,α∈(0,π).
,α∈(0,π).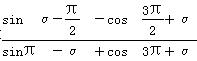 的值;
的值;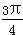 )的值.
)的值.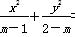 =1表示的焦点在y轴上的椭圆,且p是q的充分不必要条件,a的取值范围为________.
=1表示的焦点在y轴上的椭圆,且p是q的充分不必要条件,a的取值范围为________. 表示的平面区域是一个三角形,则a的取值范围是________.
表示的平面区域是一个三角形,则a的取值范围是________.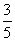 .
.