题目内容
1.已知函数f(x)=|x+1|+|x-5|的最小值为m(1)求m的值;
(2)若a,b,c为正实数,且a+b+c=m,求证:a2+b2+c2≥12.
分析 (1)通过讨论x的范围,求出f(x)的最小值即m的值即可;
(2)根据(a2+b2+c2)(12+12+12)≥(a+b+c)2=36,可得 a2+b2+c2 的最小值为12.
解答 解:(1)f(x)=|x+1|+|x-5|,
x≥5时,f(x)=x+1+x-5=2x-4,此时f(x)的最小值是6,
-1≤x≤5时,f(x)=x+1-x+5=6,
x≤-1时,f(x)=-x-1-x+5=-2x+4,此时f(x)的最小值是6,
故f(x)的最小值是6,故m=6;
(2)由(1)得a+b+c=6,
因为a,b,c 均为正实数,由柯西不等式得,
(a2+b2+c2)(12+12+12)≥(a+b+c)2=36,当且仅当a=b=c=2时等号成立,
∴a2+b2+c2 的最小值为12.
点评 本题考查了解绝对值不等式问题,考查柯西不等式的应用,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若直线y=2x上存在点(x,y)满足约束条件$\left\{\begin{array}{l}{x+y+6>0}\\{2x-y+8≥0}\\{x≤m}\end{array}\right.$,则实数m的取值范围是( )
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-∞,-2) | D. | (-∞,-2] |
12.一个几何体的三视图如图所示,则这个几何体的( )
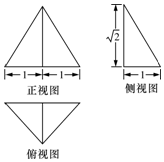

| A. | 外接球的体积为12$\sqrt{3}$ π | B. | 外接球的表面积为4π | ||
| C. | 体积为$\sqrt{2}$ | D. | 表面积为$\sqrt{5}$+$\sqrt{2}$+1 |
13. 执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )
执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )
 执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )
执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )| A. | 15 | B. | 12 | C. | 3 | D. | 180 |
11.执行如图所示的程序框图,则输出S的值是( )


| A. | 145 | B. | 148 | C. | 278 | D. | 285 |
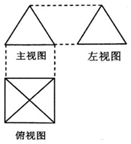 如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.
如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.