题目内容
20.已知圆C的圆心为(-1,-3),且它与x轴相切.(1)求圆的方程;
(2)若圆C被直线l:y=kx截得的弦长为$2\sqrt{7}$,求k的值.
分析 (1)根据切线的性质可知圆半径为3,从而得出圆的方程;
(2)利用垂径定理得出圆心到直线l的距离,再根据点到直线的距离列方程解出k.
解答 解:(1)圆的半径r=3,
∴圆的方程为(x+1)2+(y+3)2=9,
(2)由垂径定理可知圆心C(-1,-3)到直线l的距离d=$\sqrt{{r}^{2}-(\frac{2\sqrt{7}}{2})^{2}}$=$\sqrt{2}$,
∴$\frac{|-k+3|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$,解得k=1或k=-7.
点评 本题考查了圆的方程,直线与圆的位置关系,属于基础题.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
15.若直线y=2x上存在点(x,y)满足约束条件$\left\{\begin{array}{l}{x+y+6>0}\\{2x-y+8≥0}\\{x≤m}\end{array}\right.$,则实数m的取值范围是( )
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-∞,-2) | D. | (-∞,-2] |
8.函数$y=sin(x+\frac{π}{4})$在闭区间( )上为增函数.
| A. | $[-\frac{3}{4}π,\frac{π}{4}]$ | B. | [-π,0] | C. | $[-\frac{π}{4},\frac{3}{4}π]$ | D. | $[-\frac{π}{2},\frac{π}{2}]$ |
5.设随机变量X的分布列为P(X=k)=$\frac{k}{25}$,k=1,2,3,4,5,则P($\frac{1}{2}$<X<$\frac{5}{2}$)等于( )
| A. | $\frac{2}{15}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{15}$ |
12.一个几何体的三视图如图所示,则这个几何体的( )
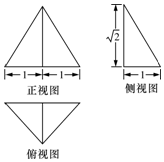

| A. | 外接球的体积为12$\sqrt{3}$ π | B. | 外接球的表面积为4π | ||
| C. | 体积为$\sqrt{2}$ | D. | 表面积为$\sqrt{5}$+$\sqrt{2}$+1 |
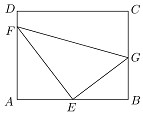 如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.
如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.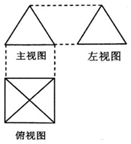 如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.
如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.