题目内容
若F1,F2为椭圆的两个焦点,过F2的直线交椭圆于P,Q两点,PF1⊥PQ,且4|PF1|=3|PQ|,则椭圆的离心率为 .
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:如图所示,设|QF2|=m,|PF2|=n,利用椭圆的定义可得|QF1|=2a-m,|PF1|=2a-n.由4|PF1|=3|PQ|,可得4(2a-n)=3(m+n).由PF1⊥PQ,利用勾股定理可得:(2a-n)2+n2=4c2,(2a-n)2+(m+n)2=(2a-m)2.
联立解得即可.
联立解得即可.
解答:
解:如图所示,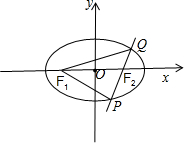
设|QF2|=m,|PF2|=n,则|QF1|=2a-m,|PF1|=2a-n.
∵4|PF1|=3|PQ|,∴4(2a-n)=3(m+n),
∵PF1⊥PQ,
∴(2a-n)2+n2=4c2,
(2a-n)2+(m+n)2=(2a-m)2.
联立
,化为n=a,代入可得a2=2c2.
解得e=
.
故答案为:
.

设|QF2|=m,|PF2|=n,则|QF1|=2a-m,|PF1|=2a-n.
∵4|PF1|=3|PQ|,∴4(2a-n)=3(m+n),
∵PF1⊥PQ,
∴(2a-n)2+n2=4c2,
(2a-n)2+(m+n)2=(2a-m)2.
联立
|
解得e=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了椭圆的定义及其性质、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 某同学进入高二前,高一年的四次期中、期末测试的数学成绩的茎叶图如图所示,则该同学数学成绩的平均数是( )
某同学进入高二前,高一年的四次期中、期末测试的数学成绩的茎叶图如图所示,则该同学数学成绩的平均数是( )| A、125 | B、126 |
| C、127 | D、128 |
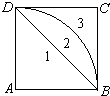 正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧
正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧 |
| DB |
| A、2:1:1 |
| B、1:2:1 |
| C、1:1:1 |
| D、2:2:1 |
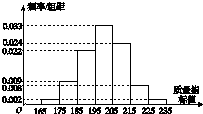 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.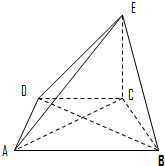 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.