题目内容
在直角坐标系xoy中,曲线C的参数方程为
(θ为参数).若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,曲线M的极坐标方程为ρsin(θ-
)=
a(其中a为常数)
(1)当a=
时,曲线M与曲线C有两个交点A,B.求|AB|的值;
(2)若曲线M与曲线C只有一个公共点,求a的取值范围.
|
| π |
| 4 |
| ||
| 2 |
(1)当a=
| 9 |
| 10 |
(2)若曲线M与曲线C只有一个公共点,求a的取值范围.
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把直线的极坐标方程化为直角坐标方程,曲线C的参数方程化为普通方程.
(1)直线与抛物线方程联立可得根与系数的关系、弦长公式即可得出.
(2)曲线M与曲线C只有一个交点.分类讨论:相切与相交时,结合图形即可得出.
(1)直线与抛物线方程联立可得根与系数的关系、弦长公式即可得出.
(2)曲线M与曲线C只有一个交点.分类讨论:相切与相交时,结合图形即可得出.
解答:
解:∵C的方程是
,消去参数θ,得y2=4x(0≤x≤2),
曲线M的方程ρsin(θ-
)=
a,
即
ρsinθ-
ρcosθ=
a,化为直角坐标方程为:x-y+a=0,
(1)当a=
时,联立
化简得:x2-
x+
=0,
∴
,
即|AB|=
=
.
(2)曲线M与曲线C只有一个交点.
①?相切时,将y=x+a代入y2=4x(0≤x≤2),
得x2+(2a-4)x+a2=0只有一个解,
∴△=(2a-4)2-4a2=0得a=1,
②?相交时,如图:-2
-2≤a<2
-2,
综上:曲线M与曲线C只有一个交点时a=1或 -2
-2≤a<2
-2.
|
曲线M的方程ρsin(θ-
| π |
| 4 |
| ||
| 2 |

即
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(1)当a=
| 9 |
| 10 |
|
化简得:x2-
| 11 |
| 5 |
| 81 |
| 100 |
∴
|
即|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
4
| ||
| 5 |
(2)曲线M与曲线C只有一个交点.
①?相切时,将y=x+a代入y2=4x(0≤x≤2),
得x2+(2a-4)x+a2=0只有一个解,
∴△=(2a-4)2-4a2=0得a=1,
②?相交时,如图:-2
| 2 |
| 2 |
综上:曲线M与曲线C只有一个交点时a=1或 -2
| 2 |
| 2 |
点评:本题考查了把直线的极坐标方程化为直角坐标方程、曲线C的参数方程化为普通方程、直线与抛物线相交可得根与系数的关系、弦长公式、直线与抛物线相切问题,考查了数形结合、分类讨论的思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知函数f(x)=|ax-1|与g(x)=(a-1)x的图象没有交点,那么实数a的取值范围是( )
| A、(-∞,0] | ||
B、(0,
| ||
C、[
| ||
| D、[1,+∞) |
复数:
=( )
| 2+i |
| 1-2i |
| A、-i | ||
| B、i | ||
C、2
| ||
D、-2
|
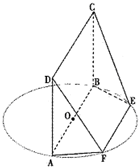 AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.
AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.