题目内容
已知集合A={x||x|≤a},B={x|x2+x-6≥0},若A∪B=R,则实数a的取值范围是 .
考点:集合的包含关系判断及应用
专题:集合
分析:根据绝对值不等式和一元二次不等式的解法求出集合A,B,利用条件A∪B=R,列出不等式组,则实数a的取值范围.
解答:
解:∵集合A={x||x|≤a},
∴①a=0,A={0}
②a<0,A=Φ
③a>0,A=[-a,a]
∵B={x|x2+x-6≥0},
∴B=(-∞,-3]∪[2,+∞)
∵若A∪B=R,
∴
则实数a的取值范围是:a≥3
故答案为:a≥3
∴①a=0,A={0}
②a<0,A=Φ
③a>0,A=[-a,a]
∵B={x|x2+x-6≥0},
∴B=(-∞,-3]∪[2,+∞)
∵若A∪B=R,
∴
|
则实数a的取值范围是:a≥3
故答案为:a≥3
点评:本题主要考查集合的相等等基本运算,属于基础题.要正确判断两个集合间相等的关系,必须对集合的相关概念有深刻的理解,善于抓住代表元素,认清集合的特征.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知A、B、C是单位圆上三个互不相同的点.若|
|=|
|,则
•
的最小值是( )
| AB |
| AC |
| AB |
| AC |
| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
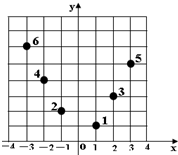 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示:
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示: