题目内容
 如图:某游乐园的摩天轮最高点距离地面108米,直径是98米,匀速旋转一圈需要18分钟,如果某人从摩天轮的最低处登上摩天轮并开始计时.
如图:某游乐园的摩天轮最高点距离地面108米,直径是98米,匀速旋转一圈需要18分钟,如果某人从摩天轮的最低处登上摩天轮并开始计时.(1)当此人第四次距离地面
| 69 |
| 2 |
(2)当此人距离地面不低于59+
| 49 |
| 2 |
| 3 |
考点:在实际问题中建立三角函数模型
专题:计算题,作图题,三角函数的图像与性质
分析:(1)如图建立平面直角坐标系,设此人登上摩天轮t分钟时距地面ym;从而写出y=108-
-49cos
t=-49cos
t+59;从而令-49cos
t+59=
可得t=18k±3,k∈Z;从而求得;
(2)由题意,-49cos
t+59≥59+
,即cos
t≤-
;在第一个周期内求即可.
| 98 |
| 2 |
| π |
| 9 |
| π |
| 9 |
| π |
| 9 |
| 69 |
| 2 |
(2)由题意,-49cos
| π |
| 9 |
| 49 |
| 2 |
| 3 |
| π |
| 9 |
| ||
| 2 |
解答:
 解:(1)如图建立平面直角坐标系,
解:(1)如图建立平面直角坐标系,
设此人登上摩天轮t分钟时距地面ym;
则α=
t=
t;
由y=108-
-49cos
t
=-49cos
t+59(t≥0);
令-49cos
t+59=
得,
cos
t=
,
故
t=2kπ±
;
故t=18k±3,k∈Z;
故t=3,15,21,33;
故当此人第四次距离地面
米时用了33分钟;
(2)由题意,-49cos
t+59≥59+
,
即cos
t≤-
;
故不妨在第一个周期内求即可,
故
≤
t≤
;
故
≤t≤
;
故
-
=3;
故摩天轮旋转一圈中有3分钟可以看到乐园的全貌.
 解:(1)如图建立平面直角坐标系,
解:(1)如图建立平面直角坐标系,设此人登上摩天轮t分钟时距地面ym;
则α=
| 2π |
| 18 |
| π |
| 9 |
由y=108-
| 98 |
| 2 |
| π |
| 9 |
=-49cos
| π |
| 9 |
令-49cos
| π |
| 9 |
| 69 |
| 2 |
cos
| π |
| 9 |
| 1 |
| 2 |
故
| π |
| 9 |
| π |
| 3 |
故t=18k±3,k∈Z;
故t=3,15,21,33;
故当此人第四次距离地面
| 69 |
| 2 |
(2)由题意,-49cos
| π |
| 9 |
| 49 |
| 2 |
| 3 |
即cos
| π |
| 9 |
| ||
| 2 |
故不妨在第一个周期内求即可,
故
| 5π |
| 6 |
| π |
| 9 |
| 7π |
| 6 |
故
| 15 |
| 2 |
| 21 |
| 2 |
故
| 21 |
| 2 |
| 15 |
| 2 |
故摩天轮旋转一圈中有3分钟可以看到乐园的全貌.
点评:本题考查了三角函数的在实际问题中的应用,属于中档题.

练习册系列答案
相关题目
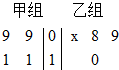 以下茎叶图记录了甲、乙两组各四名同学的植树棵树. 乙组记录中有一个数据模糊,无法辨认,在图中以X表示.
以下茎叶图记录了甲、乙两组各四名同学的植树棵树. 乙组记录中有一个数据模糊,无法辨认,在图中以X表示.