题目内容
8.若定义域为R的偶函数y=f(x)满足f(x+2)+f(x)=0,且当x∈[0,2]时,f(x)=2-x2,则方程f(x)=2sinx在[-3π,3π]内根的个数是5.分析 先求得偶函数f(x)的周期为4,根据当x∈[0,2]时,f(x)=2-x2,再画出y=f(x)以及y=2sinx在[-3π,3π]内的图象,数形结合可得结论.
解答 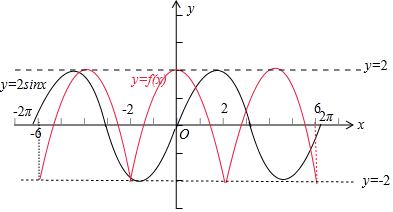 解:定义域为R的偶函数y=f(x)满足f(x+2)+f(x)=0,即足f(x+2)=-f(x),
解:定义域为R的偶函数y=f(x)满足f(x+2)+f(x)=0,即足f(x+2)=-f(x),
∴f(x+4)=f(x),故f(x)的周期为4.
且当x∈[0,2]时,f(x)=2-x2,则当x∈[-2,2]时,f(x)=2-x2 .
再画出y=f(x)以及y=2sinx在[-3π,3π]内的图象,如图所示:
数形结合可得函数y=f(x)的图象和函数y=2sinx在[-3π,3π]内的图象的交点个数为5个,
则方程f(x)=2sinx在[-3π,3π]内根的个数是5,
故答案为:5.
点评 本题主要考查函数的奇偶性以及函数的周期性,方程的根的存在性以及个数判断,函数的图象,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知函数$f(x)=2sin(\frac{π}{4}-2x)$,则函数f(x)的单调递减区间为( )
| A. | $[{\frac{3π}{8}+2kπ,\frac{7π}{8}+2kπ}](k∈Z)$ | B. | $[{-\frac{π}{8}+2kπ,\frac{3π}{8}+2kπ}](k∈Z)$ | ||
| C. | $[{\frac{3π}{8}+kπ,\frac{7π}{8}+kπ}](k∈Z)$ | D. | $[{-\frac{π}{8}+kπ,\frac{3π}{8}+kπ}](k∈Z)$ |
16. 某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:
某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:
(1)求该作物的年收获量 y关于它“相近”作物的株数x的线性回归方程;
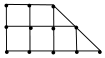
(2)农科所在如图所示的直角梯形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,图中
每个小正方形的边长均为 1,若从直角梯形地块的边界和内部各随机选取一株该作物,求这两株作物“相
近”且年产量仅相差3kg的概率.
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘估
计分别为,$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$a=\overline y-b\overline x$.
 某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:
某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:| x | 1 | 2 | 3 | 5 | 6 | 7 |
| y | 60 | 55 | 53 | 46 | 45 | 41 |
(2)农科所在如图所示的直角梯形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,图中
每个小正方形的边长均为 1,若从直角梯形地块的边界和内部各随机选取一株该作物,求这两株作物“相
近”且年产量仅相差3kg的概率.
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘估
计分别为,$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$a=\overline y-b\overline x$.
3.复数$\frac{1-2i}{2+i}$=( )
| A. | -i | B. | i | C. | $\frac{4}{5}-i$ | D. | $\frac{4}{5}-\frac{3}{5}i$ |
13.设x,y满足约束条件$\left\{\begin{array}{l}x+y≥2\\ x-y≤2\\ y≥1\end{array}\right.$,则目标函数z=x+2y的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
20.已知x,y满足$\left\{\begin{array}{l}x+y-2≥0\\ x-y+{m^2}≥0\\ x≤2\end{array}\right.$若目标函数z=-2x+y的最大值不超过2,则实数m的取值范围是( )
| A. | (-2,2) | B. | [0,2] | C. | [-2,0] | D. | [-2,2] |
17.已知曲线y=x3在点(1,1)处的切线与直线ax+y+1=0垂直,则a的值是( )
| A. | -1 | B. | 1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |