题目内容
13．设x，y满足约束条件$\left\{\begin{array}{l}x+y≥2\\ x-y≤2\\ y≥1\end{array}\right.$，则目标函数z=x+2y的最小值为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 先根据条件画出可行域，设z=x+2y，再利用几何意义求最值，将最小值转化为y轴上的截距最大，只需求出直线z=x+2y，取得截距的最小值，从而得到z最小值即可．
解答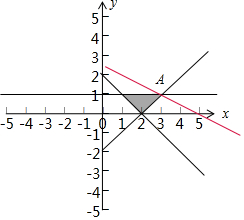 
解：作出x，y满足约束条件$\left\{\begin{array}{l}x+y≥2\\ x-y≤2\\ y≥1\end{array}\right.$，所表示的平面区域，由z=x+2y可得y=-$\frac{1}{2}$x+$\frac{1}{2}$z，
则$\frac{1}{2}$z为直线y=-$\frac{1}{2}$x+$\frac{1}{2}$z，
在y轴上的截距，截距越小，z越小，
做直线L：x+2y=0，然后把直线L向可行域方向平移，当经过点A时，z最小，
由$\left\{\begin{array}{l}{y=1}\\{x-y=2}\end{array}\right.$可得A（3，1），此时z=5，
故选：C．
点评 借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．线性规划中的最优解，通常是利用平移直线法确定．
练习册系列答案
相关题目
3．已知P为圆C：x2+y2=π2内任意一点，则点P落在函数f（x）=sinx的图象与x轴围成的封闭区域内的概率为（ ）
| A． | 0 | B． | 1 | C． | $\frac{2}{π^3}$ | D． | $\frac{4}{π^3}$ |
4．已知某蔬菜商店买进的土豆x（吨）与出售天数y（天）之间的关系如表所示：
（Ⅰ）请根据表中数据在所给网格中绘制散点图；
（Ⅱ）请根据表中提供的数据，用最小二乘法求出y关于x的线性回归方程$\widehaty=\widehatbx+\widehata$（其中$\widehatb$保留2位有效数字）；
（Ⅲ）根据（Ⅱ）中的计算结果，若该蔬菜商店买进土豆40吨，则预计可以销售多少天（计算结果保留整数）？
附：$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．
| x | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| y | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（Ⅰ）请根据表中数据在所给网格中绘制散点图；
（Ⅱ）请根据表中提供的数据，用最小二乘法求出y关于x的线性回归方程$\widehaty=\widehatbx+\widehata$（其中$\widehatb$保留2位有效数字）；
（Ⅲ）根据（Ⅱ）中的计算结果，若该蔬菜商店买进土豆40吨，则预计可以销售多少天（计算结果保留整数）？
附：$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．
18．“|x-1|+|x+2|≤5”是“-3≤x≤2”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |