题目内容
2.设不等式组$\left\{\begin{array}{l}0≤x≤2\\ 0≤y≤2\end{array}\right.$表示的平面区域为D,在区域D内随机取一点M,则点M落在圆(x-1)2+y2=1内的概率为( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 作出不等式组对应的平面区域,求出对应的面积,结合几何概型的概率公式进行求解即可.
解答  解:作出不等式组对应的平面区域,则平面区域为D的面积S=2×2=4,
解:作出不等式组对应的平面区域,则平面区域为D的面积S=2×2=4,
点M落在圆(x-1)2+y2=1内面积S=$\frac{1}{2}×π×{1}^{2}=\frac{π}{2}$,
则在区域D内随机取一点M,则点M落在圆(x-1)2+y2=1内的概率P=$\frac{\frac{π}{2}}{4}$=$\frac{π}{8}$,
故选:A.
点评 本题主要考查几何概型的概率的计算,利用线性规划的知识作出对应的平面区域求出对应的面积是解决本题的关键.

练习册系列答案
相关题目
17.下列四个命题,其中是真命题的是( )
| A. | “两个全等三角形的周长相等”的逆命题 | |
| B. | “若一个整数的末位数字是0,则这个整数能被2整除”的否命题 | |
| C. | “对顶角相等”的逆否命题 | |
| D. | ?x0∈R,x02-x0+1<0 |
14. 某校为了分析学生身体发育的状况,从一次体检中随机抽取了高三男生中20人的数据,将身高(单位:cm)用茎叶图记录如图;由此表估计该校高三男生身高在[165,175]的概率为( )
某校为了分析学生身体发育的状况,从一次体检中随机抽取了高三男生中20人的数据,将身高(单位:cm)用茎叶图记录如图;由此表估计该校高三男生身高在[165,175]的概率为( )
 某校为了分析学生身体发育的状况,从一次体检中随机抽取了高三男生中20人的数据,将身高(单位:cm)用茎叶图记录如图;由此表估计该校高三男生身高在[165,175]的概率为( )
某校为了分析学生身体发育的状况,从一次体检中随机抽取了高三男生中20人的数据,将身高(单位:cm)用茎叶图记录如图;由此表估计该校高三男生身高在[165,175]的概率为( )| A. | $\frac{3}{5}$ | B. | $\frac{9}{20}$ | C. | $\frac{11}{20}$ | D. | $\frac{1}{2}$ |
11.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)(ω>0)的图象与函数g(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的图象的对称中心完全相同,则φ=( )
| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{3}$ |
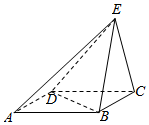 如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.