题目内容
12.已知四面体ABCD中,AB=CD=2,E、F分别为BC、AD的中点,且异面直线AB与CD所成的角为$\frac{π}{3}$,则EF=1或$\sqrt{3}$.分析 取BD中点O,连结EO、FO,推导出EO=FO=1,$∠EOF=\frac{π}{3}$,或$∠EOF=\frac{2π}{3}$,由此能求出EF.
解答 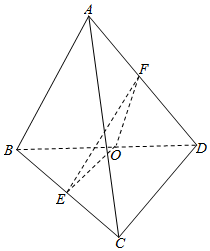 解取BD中点O,连结EO、FO,
解取BD中点O,连结EO、FO,
∵四面体ABCD中,AB=CD=2,E、F分别为BC、AD的中点,且异面直线AB与CD所成的角为$\frac{π}{3}$,
∴EO∥CD,且EO=$\frac{1}{2}CD=1$,FO∥AB,且FO=$\frac{1}{2}AB$=1,
∴∠EOF是异面直线AB与CD所成的角,
∴$∠EOF=\frac{π}{3}$,或$∠EOF=\frac{2π}{3}$,
当∠EOF=$\frac{π}{3}$时,△EOF是等边三角形,∴EF=1.
当$∠EOF=\frac{2π}{3}$时,EF=$\sqrt{{1}^{2}+{1}^{2}-\frac{1}{2}×1×1×cos\frac{2π}{3}}$=$\sqrt{3}$.
故答案为:1或$\sqrt{3}$.
点评 本题考查线段长的示法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
17.tan70°cos10°+$\sqrt{3}$sin10°tan70°-2sin50°=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
4.已知函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,若数列$\left\{{\frac{1}{f(n)}}\right\}$的前n项和为Sn,则S2015的值为( )
| A. | $\frac{4030}{4031}$ | B. | $\frac{2014}{4029}$ | C. | $\frac{2015}{4031}$ | D. | $\frac{4029}{4031}$ |
1.若$cosα=-\frac{5}{13}$,且α为第三象限角,则tanα的值等于( )
| A. | $\frac{12}{5}$ | B. | $-\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | $-\frac{5}{12}$ |
2.设不等式组$\left\{\begin{array}{l}0≤x≤2\\ 0≤y≤2\end{array}\right.$表示的平面区域为D,在区域D内随机取一点M,则点M落在圆(x-1)2+y2=1内的概率为( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
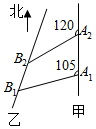 如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里?
如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里?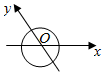 如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.
如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.